题目内容
12.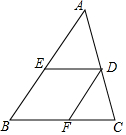 如图,在△ABC中,AB=20,BC=12,D是AC上一点,过点D作DE∥BC交AB于E,作DF∥AB交BC于F,设四边形BEDF为菱形.
如图,在△ABC中,AB=20,BC=12,D是AC上一点,过点D作DE∥BC交AB于E,作DF∥AB交BC于F,设四边形BEDF为菱形.(1)求菱形的边长;
(2)求菱形BEDF的面积与△ABC的面积之比.
分析 (1)设菱形的边长为x,则AE=20-x,CF=12-x,根据相似三角形的性质得到x=$\frac{15}{2}$,于是得到结论;
(2)根据相似三角形的性质即可得到结论.
解答 解:(1)设菱形的边长为x,则AE=20-x,CF=12-x,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AB}=\frac{DE}{BC}$,即$\frac{20-x}{20}=\frac{x}{12}$,
∴x=$\frac{15}{2}$,
∴菱形的边长是$\frac{15}{2}$;
(2)∵$\frac{{S}_{△AED}}{{S}_{△ABC}}=(\frac{DE}{BC})^{2}=\frac{25}{64}$,$\frac{{S}_{△CDF}}{{S}_{△CBA}}$=($\frac{DF}{AB}$)2=$\frac{9}{64}$,
∴菱形BEDF的面积与△ABC的面积之比=1-$\frac{25}{64}$-$\frac{9}{64}$=$\frac{15}{32}$.
点评 本题考查了相似三角形的判定和性质,菱形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2.下列事件中,是必然事件的是( )
| A. | 380人中有两个人的生日在同一天 | B. | 两条线段可以组成一个三角形 | ||
| C. | 打开电视机,它正在播放新闻联播 | D. | 三角形的内角和等于360° |
3.直角三角形的两条边长分别是5和12,则斜边上的中线长是( )
| A. | 6 | B. | 6.5 | C. | 6或 6.5 | D. | 6或 2.5 |
20.关于二次函数y=2x2-1说法正确的是( )
| A. | 有最大值-1 | B. | 有最大值2 | C. | 有最小值-1 | D. | 有最小值2 |

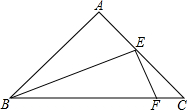 如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.
如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.