题目内容
13.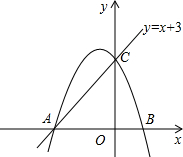 如图,已知二次函数y=-x2-2x+3的图象交x轴于A、B两点(A在B左边),交y轴于C点.
如图,已知二次函数y=-x2-2x+3的图象交x轴于A、B两点(A在B左边),交y轴于C点.(1)求A、B、C三点的坐标和直线AC的解析式;
(2)点P是直线AC上方抛物线上一动点(不与A,C重合),过点P作x轴平行线交直线AC于M点,求线段PM的最大值.
分析 (1)根据抛物线与坐标轴的交点特点.分别令x=0,y=0,求出点A、B、C的坐标;再用待定系数法求直线AC的解析式;
(2)设点P的坐标为(a,-a2-2a+3),由点P和点M的纵坐标相等,求点M的横坐标,然后可得PM=-a2-3a,根据二次函数的顶点坐标公式,求出PM的最大值即可.
解答 解:(1)令y=0,得:-x2-2x+3=0,解得:x1=-3,x2=1,
∴点A(-3,0),点B(1,0);
令x=0,得:y=3,
∴点C(0,3);
设直线AC的解析式为:y=kx+b,点A(-3,0),点C(0,3)在直线AC上,
$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线AC的解析式为:y=x+3.
(2)如图所示,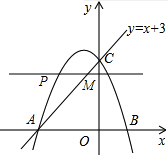
设点P的坐标为(a,-a2-2a+3),
由PM∥x轴,可知点M的纵坐标为-a2-2a+3,
∴x+3=-a2-2a+3,
∴x=-a2-2a,
∴PM=-a2-2a-a=-a2-3a(-3<a<0),
当a=$-\frac{b}{2a}=-\frac{-3}{-2}=-\frac{3}{2}$时,PM最大=$\frac{9}{4}$.
点评 本题主要考查抛物线与坐标轴的交点、二次函数的最值,在第二小题中,用含a的式子表示出点P和点M的横坐标是解决此题的关键.

练习册系列答案
相关题目
1.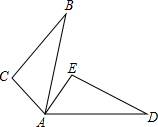 已知:如图,△ABC≌△ADE,AB与AD是对应边,AC与AE是对应边,若∠B=31°,∠C=95°,∠EAB=20°,则∠BAD等于( )
已知:如图,△ABC≌△ADE,AB与AD是对应边,AC与AE是对应边,若∠B=31°,∠C=95°,∠EAB=20°,则∠BAD等于( )
 已知:如图,△ABC≌△ADE,AB与AD是对应边,AC与AE是对应边,若∠B=31°,∠C=95°,∠EAB=20°,则∠BAD等于( )
已知:如图,△ABC≌△ADE,AB与AD是对应边,AC与AE是对应边,若∠B=31°,∠C=95°,∠EAB=20°,则∠BAD等于( )| A. | 77° | B. | 74° | C. | 47° | D. | 44° |
8.下列各组数中,不相等的是( )
| A. | -(+3)和+(-3) | B. | -5和-(+5) | C. | +(-7)和-7 | D. | +(-$\frac{2}{3}$)和+$\frac{2}{3}$ |
3.要使式子$\frac{\sqrt{a+2}}{a}$有意义,则a的取值范围是( )
| A. | a≠0 | B. | a>-2且 a≠0 | C. | a>-2或 a≠0 | D. | a≥-2且 a≠0 |
 如图,在梯形ABCD中,AB∥CD,DE⊥AB于点E,F是BC的中点,且BE+CD=EF,则∠DEF=30°.
如图,在梯形ABCD中,AB∥CD,DE⊥AB于点E,F是BC的中点,且BE+CD=EF,则∠DEF=30°.