题目内容
 如图,⊙O的半径OC与直径AB互相垂直,F是OC的中点,弦DE经过点F,若DE∥AB,∠ABD的度数是多少?
如图,⊙O的半径OC与直径AB互相垂直,F是OC的中点,弦DE经过点F,若DE∥AB,∠ABD的度数是多少?考点:含30度角的直角三角形,圆的认识
专题:
分析:连接OD,根据直角三角形中30°角所对直角边是斜边一半可证∠ODE=30°,再证∠BDE=∠ABD和∠ODB=∠ABD即可解题.
解答:解:连接OD,

∵F为中点,
∴OF=
OC=
OD,
∵OF⊥AB,DE∥AB,
∴OF⊥DE
∴∠OFD=90°
∵OF=
OD
∴∠OFD=30°
∵DE∥AB,
∴∠BDE=∠ABD
∵OD=OB
∴∠ABD=∠ODB
∴∠BDE=∠ODB,
∴∠ABD=∠BDE=15°.

∵F为中点,
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
∵OF⊥AB,DE∥AB,
∴OF⊥DE
∴∠OFD=90°
∵OF=
| 1 |
| 2 |
∴∠OFD=30°
∵DE∥AB,
∴∠BDE=∠ABD
∵OD=OB
∴∠ABD=∠ODB
∴∠BDE=∠ODB,
∴∠ABD=∠BDE=15°.
点评:本题考查了直角三角形中30°角所对直角边是斜边一半的性质,考查了等腰三角形底角相等的性质,本题中求∠OFD的大小是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
两个五次多项式相加,所得结果的次数是( )
| A、5 | B、10 |
| C、不大于5 | D、不小于5 |
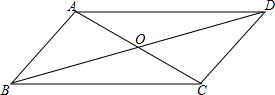 已知?ABCD的周长为68cm,对角线交于点O,△ABO与△ADO的周长和等于80cm,两对角线的长度之比是2:3,求两条对角线的长度.
已知?ABCD的周长为68cm,对角线交于点O,△ABO与△ADO的周长和等于80cm,两对角线的长度之比是2:3,求两条对角线的长度.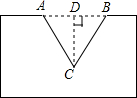 如图,工件上有一V型陶(AC=BC),测得它的上口宽20毫米,深19.2毫米,求V型角∠ACB的度数.
如图,工件上有一V型陶(AC=BC),测得它的上口宽20毫米,深19.2毫米,求V型角∠ACB的度数. 如图,△ABC内接于⊙O,且AB=BC=AC,M是
如图,△ABC内接于⊙O,且AB=BC=AC,M是