Question

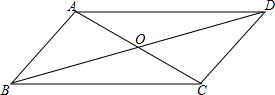已知?ABCD的周长为68cm，对角线交于点O，△ABO与△ADO的周长和等于80cm，两对角线的长度之比是2：3，求两条对角线的长度．

Answer 1

考点：平行四边形的性质

专题：

分析：根据平行四边形对角线互相平分可得OA=OC，根据平行四边形的周长求出AB+AD，设两对角线长分别为2k、3k，再利用△ABO与△ADO的周长和列方程求出k，然后解答即可．

解答：解：在?ABCD中，OA=OC，
∵?ABCD的周长为68cm，
∴AB+AD=68÷2=34cm，
设两对角线的长度分别为2k，3k，
则△ABO与△ADO的周长和=AB+OB+AO+AO+OD+AD，
=AB+AD+2AO+BD，
=34+2k+3k，
所以，34+2k+3k=80，
解得k=9.2，
2k=2×9.2=18.4cm，
3k=3×9.2=27.6cm，
所以，两对角线长分别为18.4cm，27.6cm．

点评：本题考查了平行四边形的性质，三角形的周长，利用“设k法”求解更简便，关键在于列出关于k的方程．