题目内容
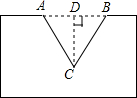如图，工件上有一V型陶（AC=BC），测得它的上口宽20毫米，深19.2毫米，求V型角∠ACB的度数．考点：解直角三角形的应用
专题：
分析：利用锐角三角函数关系结合等腰三角形的性质得出即可．
解答：解：由题意可得：BD=10毫米，DC=19.2毫米，
则tan∠DCB=
=
≈0.521，
故∠DCB≈27.5°，
则V型角∠ACB的度数为：27.5°×2=55°．
则tan∠DCB=
| BD |
| DC |
| 10 |
| 19.2 |
故∠DCB≈27.5°，
则V型角∠ACB的度数为：27.5°×2=55°．
点评：此题主要考查了解直角三角形的应用，得出正确记忆锐角三角函数关系是解题关键．
练习册系列答案
相关题目
若一个直角三角形两直角边之比为3：4，斜边长20cm，则此三角形的两直角边的长分别为（ ）
| A、9cm，12cm |
| B、12cm，16cm |
| C、6cm，8cm |
| D、3cm，4cm |
如图，⊙O的半径OC与直径AB互相垂直，F是OC的中点，弦DE经过点F，若DE∥AB，∠ABD的度数是多少？正六边形的边长为
，则它的半径是（ ）
| 3 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、2
|