题目内容
2.已知代数式(x-2)2-2(x+3)(x-3)-23.(1)化简该代数式;
(2)有人认为不论x取何值该代数式的值均为负数,你认为不正确(填“正确”或“不正确”),若不正确请举出一个反例加以说明.
分析 (1)首先去掉括号,再合并同类项,化简该代数式即可,注意去括号时符号的变化;
(2)首先把化简后的代数式因式分解,然后根据偶次方的非负性判断,判断出该说法不正确,再举出一个反例加以说明即可.
解答 解:(1)(x-2)2-2(x+3)(x-3)-23
=(x2-4x+4)-2(x2-9)-23
=x2-4x+4-2x2+18-23
=-x2-4x-1
(2)-x2-4x-1
=-(x2+4x+4)+3
=-(x+2)2+3
根据偶次方的非负性,可得-(x+2)2≤0,
但是-(x+2)2+3的值不一定是负数,
例如当x=-1时,
-(x+2)2+3
=-(-1+2)2+3
=-1+3
=2
所以有人认为不论x取何值该代数式的值均为负数,我认为不正确.
故答案为:不正确.
点评 (1)此题主要考查了因式分解方法的应用,以及整式的化简,要熟练掌握,解答此题的关键是注意去括号时符号的变化.
(2)此题还考查了偶次方的非负性,要熟练掌握,解答此题的关键是要明确:任意一个数的偶次方都是非负数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设A1,A2,A3,A4是数轴上的四个不同点,若|A1A3|=λ|A1A2|,|A1A4|=η|A1A2|,且$\frac{1}{λ}$+$\frac{1}{η}$=2,则称A3,A4调和分割A1,A2.已知平面上的点C,D调和分割点A,B,则( )
| A. | 点C可能是线段AB的中点 | |
| B. | 点D一定不是线段AB的中点 | |
| C. | 点C,D可能同时在线段AB上 | |
| D. | 点C,D可能同时在线段AB的延长线上 |
7. 下列图形中,哪个可以通过如图平移得到( )
下列图形中,哪个可以通过如图平移得到( )
 下列图形中,哪个可以通过如图平移得到( )
下列图形中,哪个可以通过如图平移得到( )| A. |  | B. |  | C. |  | D. |  |
 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=100°,求∠1的度数.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=100°,求∠1的度数.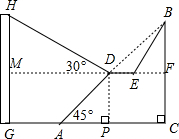 市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).
市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).