题目内容
15.若xyz≠0,且$\frac{y+z}{x}$=$\frac{z+x}{y}$=$\frac{x+y}{z}$,求分式$\frac{(y+z)(z+x)(x+y)}{xyz}$的值.分析 令$\frac{y+z}{x}$=$\frac{z+x}{y}$=$\frac{x+y}{z}$=k,则y+z=kx,z+x=ky,x+y=kz,求出k的值,再代入分式进行计算即可.
解答 解:∵令$\frac{y+z}{x}$=$\frac{z+x}{y}$=$\frac{x+y}{z}$=k,
∴y+z=kx,z+x=ky,x+y=kz,
当x+y+z=0时,x+y=-z,z+x=-y,y+z=-x,则k=-1,
当x+y+z≠0时,k=$\frac{2(x+y+z)}{x+y+z}$=2;
当k=2时,原式=$\frac{kx•ky•kz}{xyz}$=k3=23=8;
当k=-1时,原式=$\frac{kx•ky•kz}{xyz}$=k3=-13=-1.
故原式的值为8或-1.
点评 被套泥考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
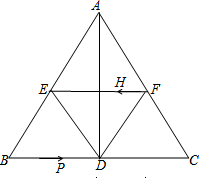 如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点. 如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.
如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.