题目内容
5. 如图,⊙O的半径为1,圆心O在正三角形的边AB的中点,⊙O向顶点A方向运动,O到A点终止,若AB=10,运动速度为1个单位/秒,运动时间设为t.试问:
如图,⊙O的半径为1,圆心O在正三角形的边AB的中点,⊙O向顶点A方向运动,O到A点终止,若AB=10,运动速度为1个单位/秒,运动时间设为t.试问:(1)当t为多少秒时,⊙O与直线AC相离?
(2)当t为多少秒时,⊙O与直线AC相切?
(3)当t为多少秒时,⊙O与直线AC相交?
分析 利用AC与⊙O相切于点D,△ABC为正三角形,可求得sin∠A=$\frac{OD}{OA}$,利用特殊角的三角函数值可求得OA的值,根据直线和圆的位置关系解答即可.
解答 解:当AC与⊙O相切于点D时, ∠ADO=90°,
∠ADO=90°,
∵△ABC为正三角形,
∴∠A=60°.
∴sin∠A=$\frac{OD}{OA}$,
OA=$\frac{2\sqrt{3}}{3}$,
(1)当0≤t<5-$\frac{2\sqrt{3}}{3}$时,⊙O与直线AC相离;
(2)当t=5-$\frac{2\sqrt{3}}{3}$时,⊙O与直线AC相切;
(3)当5-$\frac{2\sqrt{3}}{3}$<t≤5时,⊙O与直线AC相交.
点评 本题考查了圆的切线的性质及三角函数的定义的应用,直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.①直线l和⊙O相交?d<r,②直线l和⊙O相切?d=r,③直线l和⊙O相离?d>r,解题时要注意数形结合思想的运用.

练习册系列答案
相关题目
15.若|x-$\frac{1}{2}$|与(y+1)2互为相反数,则x2+y3的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{3}{4}$ |
 如图,已知△ABC各顶点的坐标分别为A(-3,2),请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各顶点坐标.
如图,已知△ABC各顶点的坐标分别为A(-3,2),请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各顶点坐标.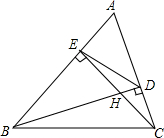 如图,△ABC中,高BD、CE相交于点H,求证:
如图,△ABC中,高BD、CE相交于点H,求证: