Question

20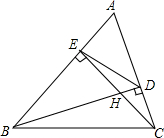．如图，△ABC中，高BD、CE相交于点H，求证：
（1）$\frac{BH}{CH}$=$\frac{EH}{DH}$；
（2）△ADE∽△ABC．

Answer 1

分析 （1）根据已知条件得到∠BEH=∠CDH=90°，由于∠BHE=∠CHD，于是得到△BHE∽△CHD，根据相似三角形的性质即可得到结论；
（2）由条件可以证明△ABD∽△ACE，则可得到$\frac{AD}{AB}=\frac{AE}{AC}$，且∠A为公共角，可证明结论．

解答 证明：（1）∵BD⊥AC，CE⊥AB，
∴∠BEH=∠CDH=90°，
∵∠BHE=∠CHD，
∴△BHE∽△CHD，
∴$\frac{BH}{CH}=\frac{EH}{HD}$；

（2）∵BD⊥AC，CE⊥AB，
∴∠ADB=∠AEC=90°，
∵∠A=∠A，
∴△ABD∽△ACE，
∴$\frac{AD}{AE}=\frac{AB}{AC}$，
∴$\frac{AD}{AB}=\frac{AE}{AC}$，
∴△ADE∽△ABC．

点评 本题主要考查相似三角形的判定和性质，掌握相似三角形的判定方法是解题的关键，注意利用相似寻找证明相似的条件．