题目内容
9．
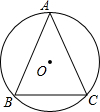如图，⊙O的半径为5，$\widehat{AB}$=$\widehat{AC}$，BC=6，求AB的长．
分析 作AE⊥BC，垂足为E，根据等腰三角形的性质、垂径定理及勾股定理求解．
解答 解：作AE⊥BC，垂足为E，连接OB，
∵$\widehat{AB}$=$\widehat{AC}$，
∴AB=AC，
根据等腰三角形的三线合一可知AE是BC的中垂线，
由垂径定理的推论得：BE=CE=$\frac{1}{2}$BC=3，又⊙O的半径为5，
由勾股定理得OE=4，则AE=9，
∴AB=$\sqrt{B{E}^{2}+A{E}^{2}}$=3$\sqrt{10}$．
点评 本题考查了等腰三角形的性质，垂径定理，勾股定理的应用，作出辅助线构建直角三角形是解题的关键．
练习册系列答案
相关题目
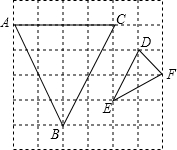如图所示，在小正方形的边长为1个单位的网格中，△ABC，△DEF的顶点都在格点上，那么△ABC与△DEF相似吗？试说明理由．
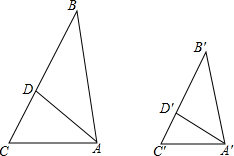如图，AD，A′D′分别为△ABC和△A′B′C′的角平分线，且AB：A′B′=BD：B′D′=AD：A′D′．试说明：△ABC∽△A′B′C′．