题目内容
1.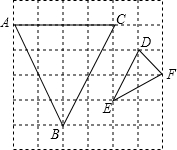 如图所示,在小正方形的边长为1个单位的网格中,△ABC,△DEF的顶点都在格点上,那么△ABC与△DEF相似吗?试说明理由.
如图所示,在小正方形的边长为1个单位的网格中,△ABC,△DEF的顶点都在格点上,那么△ABC与△DEF相似吗?试说明理由.
分析 由勾股定理求出AB=CB=2$\sqrt{5}$,DE=FE=$\sqrt{5}$,DF=$\sqrt{2}$,得出$\frac{CB}{FE}=\frac{AB}{DE}≠\frac{AC}{DF}$,即可得出结论.
解答 解:△ABC与△DEF不相似;理由如下:
由勾股定理得:AB=CB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,DE=FE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,DF=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴$\frac{CB}{FE}$=$\frac{AB}{DE}=\frac{2\sqrt{5}}{\sqrt{5}}$=2,
∵$\frac{AC}{DF}$=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
∴$\frac{CB}{FE}=\frac{AB}{DE}≠\frac{AC}{DF}$,
∴△ABC与△DEF不相似.
点评 本题考查了正方形的性质、相似三角形的判定方法、勾股定理;熟练掌握相似三角形的判定方法,由勾股定理求出相应边长是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如果a、b互为相反数,则6(a2-2a)-3(2a2+4b-1)的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
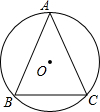 如图,⊙O的半径为5,$\widehat{AB}$=$\widehat{AC}$,BC=6,求AB的长.
如图,⊙O的半径为5,$\widehat{AB}$=$\widehat{AC}$,BC=6,求AB的长.