题目内容
16.观察下列各式:$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$;$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$;$\frac{1}{3×4}$=$\frac{1}{3}-\frac{1}{4}$;$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$;….(1)猜想它的规律:把$\frac{1}{n(n+1)}$表示出来:$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
(2)用你猜想得到的规律,计算:$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{(n-1)n}$+$\frac{1}{n(n+1)}$.
分析 (1)根据所给式子发现$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$;
(2)将$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{(n-1)n}$+$\frac{1}{n(n+1)}$化为$\frac{1}{1×2}$$+\frac{1}{2×3}$$+\frac{1}{3×4}$$+\frac{1}{4×5}$+…+$\frac{1}{(n-1)n}$+$\frac{1}{n(n+1)}$,再利用所给规律化简即可.
解答 解:(1)∵$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$;$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$;$\frac{1}{3×4}$=$\frac{1}{3}-\frac{1}{4}$;$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$;
…
∴$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$;
故答案为:$\frac{1}{n}-\frac{1}{n+1}$;
(2)∵$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$;$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$;$\frac{1}{3×4}$=$\frac{1}{3}-\frac{1}{4}$;$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$;…$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$;
∴$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{(n-1)n}$+$\frac{1}{n(n+1)}$=$\frac{1}{1×2}$$+\frac{1}{2×3}$$+\frac{1}{3×4}$$+\frac{1}{4×5}$+…+$\frac{1}{(n-1)n}$+$\frac{1}{n(n+1)}$,
=1$-\frac{1}{2}$$+\frac{1}{2}-\frac{1}{3}$$+\frac{1}{3}-\frac{1}{4}$$+\frac{1}{4}-\frac{1}{5}$+…$+\frac{1}{n-1}$$-\frac{1}{n}$$+\frac{1}{n}$$-\frac{1}{n+1}$
=1$-\frac{1}{n+1}$
=$\frac{n}{n+1}$.
点评 本题主要考查了数字的变化规律,发现规律,运用规律是解答此题的关键.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 如图,∠B=∠ADE,∠DEC=110°,则∠C等于70°.
如图,∠B=∠ADE,∠DEC=110°,则∠C等于70°. 把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=42°.
把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=42°.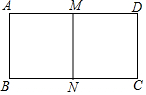 如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.
如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.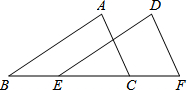 如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.
如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.