题目内容

11．把正三角形、正四边形、正五边形按如图所示的位置摆放，若∠1=52°，∠2=18°，则∠3=42°．

分析 利用360°减去等边三角形的一个内角的度数，减去正方形的一个内角的度数，减去正五边形的一个内角的度数，然后减去∠1和∠2即可求得．

解答 解：等边三角形的内角的度数是60°，正方形的内角度数是90°，正五边形的内角的度数是：$\frac{1}{5}$（5-2）×180°=108°，
则∠3=360°-60°-90°-108°-∠1-∠2=42°．
故答案是：42°．

点评 本题考查了多边形的外角和定理，正确理解∠3等于360°减去等边三角形的一个内角的度数，减去正方形的一个内角的度数，减去正五边形的一个内角的度数，然后减去∠1和∠2是关键．

练习册系列答案
相关题目
1．下列各式计算正确的是（　　）
A．a3•a3=a9B．a10÷a5=a2C．（2a2）2=2a4D．a0÷a-1=a
2．计算：
（1）3$\sqrt{2}$+2（$\sqrt{2}$-$\sqrt{3}$）
（2）|$\root{3}{27}$|+|-$\sqrt{16}$|+$\sqrt{2\frac{7}{9}}$-$\root{3}{512}$．
19．-12+[$\frac{7}{4}$+8×（-3）]×0.5-（-5）2．
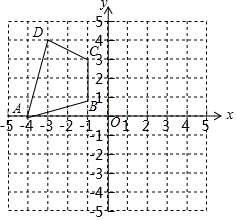6．如图，四边形ABCD的四个顶点的坐标分别为A（-4，0），B（-1，1），C（-1，3），D（-3，4），分别画出与四边形ABCD关于x轴和y轴对称的图形．
16．观察下列各式：$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$；$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$；$\frac{1}{3×4}$=$\frac{1}{3}-\frac{1}{4}$；$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$；…．
（1）猜想它的规律：把$\frac{1}{n（n+1）}$表示出来：$\frac{1}{n（n+1）}$=$\frac{1}{n}-\frac{1}{n+1}$．
（2）用你猜想得到的规律，计算：$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{（n-1）n}$+$\frac{1}{n（n+1）}$．
3．下列各图中的∠1为圆周角的是（　　）
A．B．C．D．
20．解方程：
（1）5x=3（x-2）
（2）$\frac{2x+1}{3}$-2=$\frac{1+x}{2}$．
1．如图1，在平面直角坐标系中，AB=OB=8，∠ABO=90°，∠yOC=45°，射线OC以每秒2个单位长度的速度向右平行移动，当射线OC经过点B时停止运动，设平行移动x秒后，射线OC扫过Rt△ABO的面积为S，射线平移到O′C′，且O′C′与OA相交于点G．

（1）求S关于x的函数关系式；
（2）当x为何值时，以G、O、B为顶点的三角形为等腰三角形；
（3）当x=3时，在直线O′C′是否存在点P，使得△POB绕着某一边的中点旋转180°后得到一个矩形？若存在，求P的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网