题目内容
8.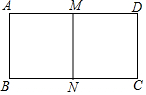 如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.
如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.
分析 矩形DMNC与矩形ABCD相似,对应边的比相等,就可以得到AD的长;
解答 解:由已知得MN=AB,MD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∵矩形DMNC与矩形ABCD相似,
$\frac{DM}{AB}$=$\frac{MN}{BC}$,
∵MN=AB,DM=$\frac{1}{2}$AD,BC=AD,
∴$\frac{1}{2}$AD2=AB2,
∴由AB=4得,AD=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$;
点评 本题考查相似多边形的性质,相似多边形的对应边的比相等.

练习册系列答案
相关题目
3.下列各图中的∠1为圆周角的是( )
| A. |  | B. |  | C. |  | D. |  |
18. 期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
收集数据
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有②、③.(只要填写序号即可)
①随机抽取一个班级的48名学生;②在全年级学生中随机抽取48名学生;③在全年级12个班中分别各抽取4名学生;④从全年级学生中随机抽取48名男生.
整理数据
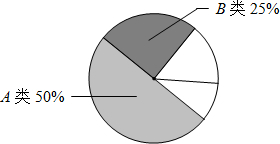
(2)将抽取的48名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为60°、30°;
②估计全年级A、B类学生大约一共有432名.
(3)学校为了解其他学校教学情况,将同层次的第一、第二两所中学的抽样数据进行对比,得下表:
你认为哪所学校的教学效果较好?结合数据,请提出一个解释来支持你的观点.
 期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:收集数据
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有②、③.(只要填写序号即可)
①随机抽取一个班级的48名学生;②在全年级学生中随机抽取48名学生;③在全年级12个班中分别各抽取4名学生;④从全年级学生中随机抽取48名男生.
整理数据
(2)将抽取的48名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为60°、30°;
②估计全年级A、B类学生大约一共有432名.
| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | $\frac{1}{2}$ | |
| B类(60~79) | $\frac{1}{4}$ | |
| C类(40~59) | 8 | $\frac{1}{6}$ |
| D类(0~39) | 4 | $\frac{1}{12}$ |
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 第一中学 | 71 | 52 | 432 | 0.75 |
| 第二中学 | 71 | 80 | 497 | 0.82 |
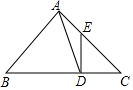 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC上一点,AB=BD,DE⊥BC,交AC于点E,则图中的等腰三角形有4个.
如图,在△ABC中,∠BAC=90°,AB=AC,D为BC上一点,AB=BD,DE⊥BC,交AC于点E,则图中的等腰三角形有4个.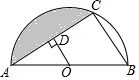 如图,O为半圆的圆心,直径AB=12,C是半圆上一点,OD⊥AC于点D,OD=3.
如图,O为半圆的圆心,直径AB=12,C是半圆上一点,OD⊥AC于点D,OD=3. 如图,四边形ABCD是平行四边形,DB⊥AD,AD=8cm,BD=12cm,求BC,AC的长.
如图,四边形ABCD是平行四边形,DB⊥AD,AD=8cm,BD=12cm,求BC,AC的长.