题目内容
12. 如图,在平面直角坐标系中,△BOC是等腰三角形,点B在x轴正半轴上,△OAD是△OBC绕点O逆时针旋转60°得到的,点A在y轴正半轴上,连接DC,线段OA的长是关于x的方程x2-4x+4=0的根
如图,在平面直角坐标系中,△BOC是等腰三角形,点B在x轴正半轴上,△OAD是△OBC绕点O逆时针旋转60°得到的,点A在y轴正半轴上,连接DC,线段OA的长是关于x的方程x2-4x+4=0的根(1)求过点O、点D的直线的解析式;
(2)求四边形OACD的面积;
(3)平面内是否存在点P,使以点D、O、B、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
分析 (1)先解方程,求得OA的长,再过点D作DH⊥y轴,根据Rt△ADH中的边角关系,求得点D的坐标,最后运用待定系数法求得过点O、点D的直线的解析式;
(2)先运用SAS判定△DOC≌△BOC,得出CD=BC,进而判定四边形AOCD是菱形,并计算菱形的面积;
(3)根据平行四边形的不同位置,分三种情况,得出点P的坐标.
解答 解:(1)解方程x2-4x+4=0,得x=2
∴OA=2
由旋转可得,AD=BC=OC=OA=2,∠AOC=60°
∵∠AOB=90°
∴∠BOC=30°
∴∠CBO=∠BOC=∠AOD=∠ADO=30°
过点D作DH⊥y轴于点H,则∠HAD=60°
在Rt△ADH中,AD=2
∴HD=$\sqrt{3}$,AH=1
∴OH=3
∴点D的坐标为($\sqrt{3}$,3)
设直线OD解析式为y=kx
将D的坐标代入,得3=$\sqrt{3}$k
∴k=$\sqrt{3}$
∴过点O、点D的直线的解析式为y=$\sqrt{3}$x
(2)∵∠BOC=∠AOD=30°
∴∠COD=30°
在△DOC和△BOC中
$\left\{\begin{array}{l}{OD=OB}\\{∠DOC=∠BOC}\\{OC=OC}\end{array}\right.$
∴△DOC≌△BOC(SAS)
∴CD=BC
∴CD=OC=OA=AD
∴四边形AOCD是菱形
∴菱形OACD的面积=AO×DH=2$\sqrt{3}$
(3)存在.连接BD,过O作BD的平行线,过B作OD的平行线,过D作OB的平行线,交于P1、P2、P3三点,则
四边形P1DOB、四边形P2OBD、四边形P3BDO均为平行四边形
由OB=OD,∠BOD=60°可知,△OBD是等边三角形
∴四边形P1DOB、四边形P2OBD、四边形P3BDO均为菱形
∴P1、P2、P3三点离x轴的距离=OH=3
如图,在Rt△ADH中,HD=$\sqrt{3}$,OH=3
∴OD=2$\sqrt{3}$
又∵P1H=P1D+DH=2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$,P2H=P2D-DH=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$
∴P1(3$\sqrt{3}$,3),P2(-$\sqrt{3}$,3)
又∵P3与D关于x轴对称,D($\sqrt{3}$,3)
∴P3($\sqrt{3}$,-3)
故点P的坐标为(3$\sqrt{3}$,3)或(-$\sqrt{3}$,3)或($\sqrt{3}$,-3)
点评 本题主要考查了几何变换中的旋转,解决问题的关键是掌握旋转的性质以及待定系数法求函数解析式的方法,解题时需要运用四边相等的四边形是菱形这一判定方法,并且注意菱形的面积等于底乘高,有时需要根据菱形对角线的长度求菱形的面积.此外,在判断平行四边形第四个顶点的位置时,需要进行分类讨论,不能遗漏.

| A. | 无实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 根的情况不确定 |
| A. | xy=2 | B. | 2x=y | C. | 2x=2 | D. | x2=y |
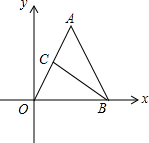 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限,点B在x轴正半轴上,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限,点B在x轴正半轴上,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点. 如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°.
如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°. 如图,四边形ABCD内接于⊙O,∠A=100°,⊙O的半径=2,则劣弧$\widehat{BD}$的长=$\frac{16π}{9}$.
如图,四边形ABCD内接于⊙O,∠A=100°,⊙O的半径=2,则劣弧$\widehat{BD}$的长=$\frac{16π}{9}$.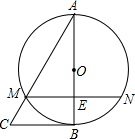 如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=$\sqrt{3}$,则弧BN的长为$\frac{2\sqrt{3}}{9}$π.
如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=$\sqrt{3}$,则弧BN的长为$\frac{2\sqrt{3}}{9}$π.