题目内容
9. 如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,点D是BA延长线上一点,且AC=AD,若∠B=30°,AB=2,则CD的长是( )
如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,点D是BA延长线上一点,且AC=AD,若∠B=30°,AB=2,则CD的长是( )| A. | $\sqrt{5}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}$ |
分析 连接OC,先根据AB是⊙O的直径得出∠ACB=90°,再由∠B=30°得出∠BAC=60°,根据AC=AD可知∠D=∠ACD,由三角形外角的性质得出∠D=∠ACD=30°,再由OC=OB,∠B=30°得出∠DOC=60°,故可得出∠OCD=90°,再由AB=2可知OC=1,根据锐角三角函数的定义即可得出结论.
解答 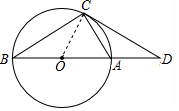 解:连接OC,
解:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠B=30°,
∴∠BAC=60°.
∵AC=AD,
∴∠D=∠ACD=30°.
∵OC=OB,∠B=30°,
∴∠DOC=60°,
∴∠OCD=90°.
∵AB=2,
∴OC=1,
∴CD=$\frac{OC}{tan30°}$=$\frac{1}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$.
故选D.
点评 本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.从国家旅游局获悉,今年国庆期间全国共接待游客5.93亿人次,将5.93亿用科学记数法表示正确的是( )
| A. | 5.93×107 | B. | 5.93×108 | C. | 5.93×109 | D. | 5.93×1010 |
14.一元二次方程5x2-11x+4=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
18.下列代数式符合书写要求的是( )
| A. | a+5 | B. | 5$\frac{3}{4}$a | C. | ab5 | D. | a÷b |

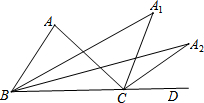 如图,在△ABC中,∠A=96°,延长BC至D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )
如图,在△ABC中,∠A=96°,延长BC至D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )