题目内容
9.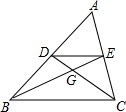 如图,点D,E分别是△ABC的边AB,AC的中点,BE交CD于G点,
如图,点D,E分别是△ABC的边AB,AC的中点,BE交CD于G点,(1)找出图中的所有相似三角形,并选一对相似加以证明
(2)求证:CG=2DG.
分析 (1)由条件可得出DE∥BC,则可得出相似的三角形;
(2)由△GDE∽△GBC,根据相似三角形的性质可证明CG=2DG.
解答 (1)解:相似的三角形有△ADE∽△ABC,△GDE∽△GBC.
选择证明△GDE∽△GBC.证明如下:
∵D、E分别是△ABC的边AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,
∴∠EDG=∠GCB,∠DEG=∠CBG,
∴△GDE∽△GBC;
(2)证明:由(1)可知△GDE∽△GBC,
∴$\frac{DE}{BC}$=$\frac{DG}{CG}$=$\frac{1}{2}$,
∴CG=2DG.
点评 本题主要考查相似三角形的判定和性质,由条件得出DE是三角形的中位线证明DE∥BC是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.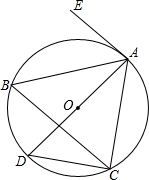 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
14.去年我市有56940名初中毕业生参加升学考试,为了了解这56940名考生的数学成绩.从中抽取2000名考生的数学成绩进行统计分析.在这个问题中样本是( )
| A. | 56940名考生 | B. | 所抽取的2000名考生的数学成绩 | ||
| C. | 56940名考生的数学成绩 | D. | 所抽取的2000名考生 |
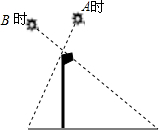 如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米.
如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米.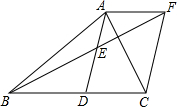 已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.
已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.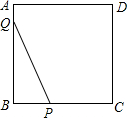 如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.
如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.