题目内容
10.已知5x=m,5y=n,则52x+3y等于( )| A. | 2m+3n | B. | m2+n2 | C. | 6mn | D. | m2n3 |
分析 直接利用同底数幂的乘法运算法则以及结合幂的乘方运算法则化简求出答案.
解答 解:∵5x=m,5y=n,
∴52x+3y=52x×53y=(5x)2×(5y)3=m2×n3=m2n3.
故选:D.
点评 本题考查了同底数幂的乘法、幂的乘方等知识,熟练掌握运算性质和法则是解题的关键.

练习册系列答案
相关题目
1.将直线y=$\frac{1}{2}$x+1向右平移4个单位后得到直线y=kx+b,则k+b的值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
18.下列计算结果为a6的是( )
| A. | a•a5 | B. | a8-a2 | C. | (a3)3 | D. | 4a8÷3a2 |
15.一个袋子中装有3个红球和2个黄球,这些球的形状、大小、质地完全相同,在看不到球的条件下,随机从袋中摸出2个球,其中2个球颜色不相同的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
2. 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )
如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )
 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )
如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )| A. | (-2m,-2n) | B. | (2m,2n) | C. | (-2n,-2m) | D. | (2n,2m) |
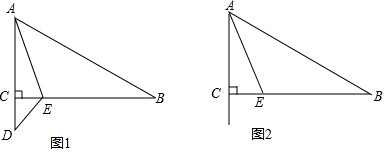
20. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )| A. | 2+$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3+$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
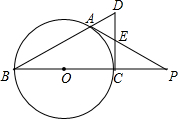 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.