题目内容
20.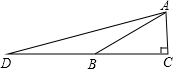 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )| A. | 2+$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3+$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 通过解直角△ABC得到AC与BC、AB间的数量关系,然后利用锐角三角函数的定义求tan∠DAC的值.
解答  解:如图,∵在△ABC中,AC⊥BC,∠ABC=30°,
解:如图,∵在△ABC中,AC⊥BC,∠ABC=30°,
∴AB=2AC,BC=$\frac{AC}{tan30°}$=$\sqrt{3}$AC.
∵BD=BA,
∴DC=BD+BC=(2+$\sqrt{3}$)AC,
∴tan∠DAC=$\frac{DC}{AC}$=$\frac{(2+\sqrt{3})AC}{AC}$=2+$\sqrt{3}$.
故选:A.
点评 本题考查了解直角三角形,利用锐角三角函数的概念解直角三角形问题.

练习册系列答案
相关题目
10.已知5x=m,5y=n,则52x+3y等于( )
| A. | 2m+3n | B. | m2+n2 | C. | 6mn | D. | m2n3 |
11. 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b | D. | a-c<b-c |
15.一元二次方程x2-2x=0根的判别式的值为( )
| A. | 4 | B. | 2 | C. | 0 | D. | -4 |
 如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.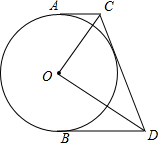 如图,已知AC,BD与⊙O相切于点A,B,且AC∥BD,若∠COD=90°,求证:CD是⊙O的切线.
如图,已知AC,BD与⊙O相切于点A,B,且AC∥BD,若∠COD=90°,求证:CD是⊙O的切线.