题目内容
17.(1)已知:a+$\frac{1}{a}$=10,求a2+$\frac{1}{{a}^{2}}$的值和${(a-\frac{1}{a})}^{2}$的值;(2)若x2-2x+y2+6y+10=0,求yx的值.
分析 (1)把a+$\frac{1}{a}$=10的两边平方得出a2+$\frac{1}{{a}^{2}}$的值,再进一步配方得出${(a-\frac{1}{a})}^{2}$的值;
(2)先利用完全平方公式把x2-2x+y2+6y+10=0,变为(x-1)2+(y+3)2=0,利用非负数的性质得出x、y的数值,进一步代入求得答案即可.
解答 解:(1)∵a+$\frac{1}{a}$=10,
∴(a+$\frac{1}{a}$)2=102,
∴a2+$\frac{1}{{a}^{2}}$=98;
∴a2+$\frac{1}{{a}^{2}}$-2=96
即${(a-\frac{1}{a})}^{2}$=96.
(2)∵x2-2x+y2+6y+10=0,
∴(x-1)2+(y+3)2=0,
∴x-1=0,y+3=0,
∴x=1,y=-3,
∴yx=-3.
点评 此题考查因式分解的实际运用,非负数的性质,掌握完全平方公式是解决问题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,是一只圆柱形的封闭易拉罐,它的底面半径为4cm,高为15cm,问易拉罐内可放的搅拌棒(直线型)最长是多长?
如图,是一只圆柱形的封闭易拉罐,它的底面半径为4cm,高为15cm,问易拉罐内可放的搅拌棒(直线型)最长是多长?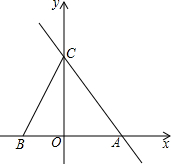 直线y=-2x+b与x轴、y轴分别交与点A、C,点B(-2,0),AB=$\frac{5}{6}$CO.
直线y=-2x+b与x轴、y轴分别交与点A、C,点B(-2,0),AB=$\frac{5}{6}$CO.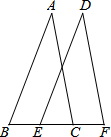 已知:如图,∠B=∠DEF,∠ACB=∠F,BE=CF.求证:AB=DE.
已知:如图,∠B=∠DEF,∠ACB=∠F,BE=CF.求证:AB=DE. 求直线y=2x+4和y=-3x+9与x轴所围成三角形的面积.
求直线y=2x+4和y=-3x+9与x轴所围成三角形的面积.