题目内容
7.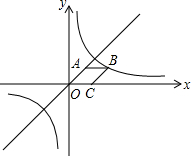 如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )
如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )| A. | 1+$\frac{{\sqrt{2}}}{2}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | 2$\sqrt{2}$ |
分析 首先根据直线y=x经过点C,设A点坐标为(a,a),再利用勾股定理算出AO=$\sqrt{2}$a,进而得到CO=CB=AB═AO=$\sqrt{2}$a,再利用菱形的面积公式计算出a的值,进而得到C点坐标,进而得到B点坐标,即可求出k的值.
解答 解:∵直线y=x经过点B,
∴设A(a,a),
∴AO2=2a2,
∴AO=$\sqrt{2}$a,
∵四边形OABC是菱形,
∴AO=CO=CB=AB=$\sqrt{2}$a,
∵菱形OABC的面积是$\sqrt{2}$,
∴$\sqrt{2}$a•a=$\sqrt{2}$,
∴a=1,
∴CB=$\sqrt{2}$,A(1,1)
∴B(1+$\sqrt{2}$,1),
∵B(1+$\sqrt{2}$,1)在反比例函数y=$\frac{k}{x}$图象上,
∴k=(1+$\sqrt{2}$)×1=1+$\sqrt{2}$,
故答案为:B.
点评 此题主要考查了待定系数法求反比例函数、菱形的面积公式、菱形的性质、勾股定理;关键是根据菱形的面积求出A点坐标,进而得到B点坐标,即可求出反比例函数解析式.

练习册系列答案
相关题目
9.若(x-2z)2+|2x-1|+|y+3|=0,则满足等式的x、y、z分别是( )
| A. | x=$\frac{1}{2}$,y=3,z=1 | B. | x=-$\frac{1}{2}$,y=-3,z=-1 | C. | x=$\frac{1}{2}$,y=-3,z=$\frac{1}{4}$ | D. | x=$\frac{1}{2}$,y=3,z=2 |
 如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是AE=AC.
如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是AE=AC.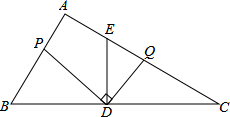 如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.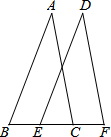 已知:如图,∠B=∠DEF,∠ACB=∠F,BE=CF.求证:AB=DE.
已知:如图,∠B=∠DEF,∠ACB=∠F,BE=CF.求证:AB=DE.