题目内容
5. 如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法).
如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法).(1)用直尺和圆规作出∠BAD的平分线AP,交BC于点P.
(2)在(1)的基础上,若∠APB=55°,求∠B的度数.
(3)在(1)的基础上,E是AP的中点,连接BE并延长,交AD于点F,连接PF.求证:四边形ABPF是菱形.
分析 (1)利用基本作图(作已知角的平分线)作AP平分∠DAB;
(2)先利用平行线的性质得∠DAP=∠APB=55°,再利用角平分线定义得∠BAP=∠DAP=55°,然后根据三角形内角和计算∠ABP的度数;
(2)先由∠BAP=∠APB得到BA=BP,再判断△ABF为等腰三角形得到AB=AF,所以AF=BP,则可判断四边形ABPF是平行四边形,然后加上AB=BP可判断四边形ABPF是菱形.
解答 (1)解:如图,AP为所作;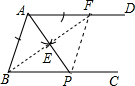
(2)解:∵AD∥BC,
∴∠DAP=∠APB=55°,
∵AP平分∠DAB,
∴∠BAP=∠DAP=55°,
∴∠ABP=180°-55°-55°=70°;
(2)证明:∵∠BAP=∠APB,
∴BA=BP,
∵BE=FE,AE平分∠BAF,
∴△ABF为等腰三角形,
∴AB=AF,
∴AF=BP,
而AF∥BP,
∴四边形ABPF是平行四边形,
∵AB=BP,
∴四边形ABPF是菱形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了菱形的判定.

练习册系列答案
相关题目
20.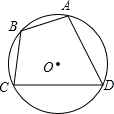 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )| A. | 2π | B. | 4π | C. | 5π | D. | 6π |
15.下列分式的值,可以为零的是( )
| A. | $\frac{{x}^{2}+1}{x-1}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | C. | $\frac{{x}^{2}+2x+1}{x+1}$ | D. | $\frac{x+1}{x-1}$ |
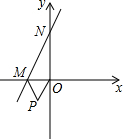 如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.
如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.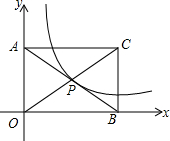 如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$.
如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$.
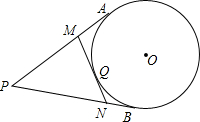 如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.
如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.