题目内容
18．先化简，再求值：（$\frac{a}{a+1}$+$\frac{a-4}{{a}^{2}-1}$）÷$\frac{a-2}{{a}^{2}-2a+1}$，其中a=3．分析 根据分式的混合运算法则、分式的通分和约分法则把原式化简，把a的值代入计算即可．
解答 解：原式=$\frac{a（a-1）+a-4}{（a+1）（a-1）}$×$\frac{（{a-1）}^{2}}{a-2}$
=$\frac{（a+2）（a-2）}{（a+1）（a-1）}$×$\frac{（a-1）^{2}}{a-2}$
=$\frac{（a+2）（a-1）}{a+1}$，
当a=3时，原式=$\frac{（3+2）（3-1）}{3+1}$=$\frac{5}{2}$．
点评 本题考查的是分式的化简求值，掌握分式的混合运算法则、分式的通分和约分法则是解题的关键．
练习册系列答案
相关题目
6．
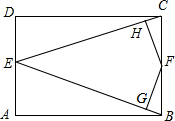如图，在矩形ABCD中，AB=3，BC=2，点E为AD中点，点F为BC边上任一点，过点F分别作EB，EC的垂线，垂足分别为点G，H，则FG+FH为（ ）
如图，在矩形ABCD中，AB=3，BC=2，点E为AD中点，点F为BC边上任一点，过点F分别作EB，EC的垂线，垂足分别为点G，H，则FG+FH为（ ）| A． | $\frac{5}{2}$ | B． | $\frac{5}{2}$$\sqrt{10}$ | C． | $\frac{3}{10}$$\sqrt{10}$ | D． | $\frac{3}{5}$$\sqrt{10}$ |
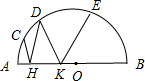如图，AB是⊙O的直径，C、D、E是⊙O上的点，H、K是直径AB上的点，若∠AHC=∠DHB，∠DKA=∠EKB，$\widehat{AC}$的度数是20°，$\widehat{BE}$的度数是50°，则∠D=55°．
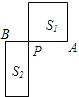如图，线段AB=1，P是AB的黄金分割点，且PA＞PB，S1表示以PA为边长的正方形面积，S2表示以AB为长、PB为宽的矩形面积，则S1-S2=0．