题目内容
5.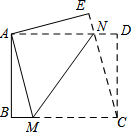 如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )| A. | 5 | B. | 4 | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
分析 首先过点N作NG⊥BC于G,由四边形ABCD是矩形,易得四边形CDNG是矩形,又由折叠的性质,可得四边形AMCN是菱形,由△CDN的面积与△CMN的面积比为1:4,根据等高三角形的面积比等于对应底的比,可得DN:CM=1:4,然后设DN=x,由勾股定理可求得MN的长,继而求得答案.
解答 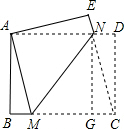 解:过点N作NG⊥BC于G,
解:过点N作NG⊥BC于G,
∵四边形ABCD是矩形,
∴四边形CDNG是矩形,AD∥BC,
∴CD=NG,CG=DN,∠ANM=∠CMN,
由折叠的性质可得:AM=CM,∠AMN=∠CMN,
∴∠ANM=∠AMN,
∴AM=AN,
∴四边形AMCN是平行四边形,
∵AM=CM,
∴四边形AMCN是菱形,
∵△CDN的面积与△CMN的面积比为1:4,
∴DN:CM=1:4,
设DN=x,
则AN=AM=CM=CN=4x,AD=BC=5x,CG=x,
∴BM=x,GM=3x,
在Rt△CGN中,NG=$\sqrt{C{N}^{2}-C{G}^{2}}$=$\sqrt{15}$x,
在Rt△MNG中,MN=$\sqrt{G{M}^{2}+N{G}^{2}}$=2$\sqrt{6}$x,
∴$\frac{MN}{BM}$=2$\sqrt{6}$,
故选D.
点评 此题考查了折叠的性质、矩形的判定与性质、菱形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意折叠中的对应关系,注意数形结合与方程思想的应用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
16.在下列黑体大写英文字母中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.已知a、b为实数,且$\sqrt{a-\frac{1}{2}}$+b2+4=4b,则a2015b2016的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
15.正三角形的内切圆与外接圆的面积的比为( )
| A. | .1:3 | B. | 1:4 | C. | 1:2 | D. | 3:4 |
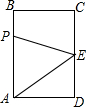 如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5. 如图,在正方形网格中,图②是由图①经过变换得到的,其旋转中心可能是点B(填“A”“B”“C”或“D”)
如图,在正方形网格中,图②是由图①经过变换得到的,其旋转中心可能是点B(填“A”“B”“C”或“D”)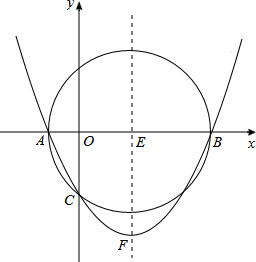 如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.
如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.