题目内容
13.关于x的方程a(x+m)2+b=0的解是x1=-3,x2=1(a、b、m均为常数,a≠0),则方程a(x+m-1)2+b=0的解是x1=-2,x2=0.分析 根据关于x的方程a(x+m)2+b=0的解是x1=-3,x2=1得出二次函数y=a(x十m)2+b与x轴的交点为(-3,0)和(1,0),把抛物线向右平移1个单位,得到抛物线y=a(x+m-1)2+b与x轴的交点,进而得出方程a(x+m+3)2=b的解即可.
解答 解:由题意可知二次函数y=a(x十m)2+b与x轴的交点为(-3,0)和(1,0),
将函数向右平移1个单位,则交点为(-2,0)和(0,0),所以方程的根为-2和0.
故答案为x1=-2,x2=0.
点评 本题考查了解一元二次方程-直接开平方法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.若a+b=2,则代数式a2-b2+4b的值是( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
18.下列等式正确的是( )
| A. | $\sqrt{49}$=±7 | B. | $\sqrt{-49}$=-7 | C. | $\root{3}{-9}$=-3 | D. | ($\sqrt{\frac{1}{2}}$)2=$\frac{1}{2}$ |
5.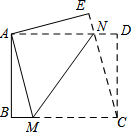 如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
 如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )| A. | 5 | B. | 4 | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
2. 如图,已知∠BAC=90°,AD⊥BC于D,则图中互余的角有( )对.
如图,已知∠BAC=90°,AD⊥BC于D,则图中互余的角有( )对.
 如图,已知∠BAC=90°,AD⊥BC于D,则图中互余的角有( )对.
如图,已知∠BAC=90°,AD⊥BC于D,则图中互余的角有( )对.| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
 如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)