题目内容
20.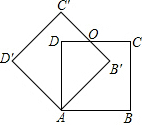 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB′C′D′,图中重合部分四边形AB′OD的面积为$\sqrt{2}$-1.
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB′C′D′,图中重合部分四边形AB′OD的面积为$\sqrt{2}$-1.
分析 根据题意可以推出△ADO≌△AB′O,所以重合部分的面积为2△ADO的面积,进而求出即可.
解答 解:连接AO,连接B′C,
∵两个正方形的边长都为1,将其中一个固定不动,另一个绕顶点A旋转45°,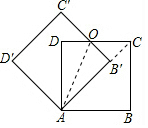
∴A,B′,C三点在一条直线上,
∴∠DAC=∠DCA=45°,
∴B′O=B′C,
在Rt△ADO和Rt△AB′O中,
$\left\{\begin{array}{l}{AD=AB′}\\{AO=AO}\end{array}\right.$,
∴Rt△ADO≌Rt△AB′O(HL),
∴OD=B′O,
设DO=x,
∴B′O=x,OC=1-x,
∴x2+x2=(1-x)2,
解得:x=-1-$\sqrt{2}$(不合题意舍去),或x=-1+$\sqrt{2}$,
∴四边形AB′OD的面积=2S△AC′M=2×$\frac{1}{2}$×1×(-1+$\sqrt{2}$)=$\sqrt{2}$-1,
故答案为:$\sqrt{2}$-1.
点评 本题考查了旋转的性质,正方形的性质定理、三角形的面积、全等三角形的判定和性质.解题关键在于求出DO=B′O的长度.

练习册系列答案
相关题目
11.已知y是x的二次函数,函数y与自变量x的对应值如表:
该二次函数图象向左平移3个单位,图象经过原点.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
5.正比例函数y=kx的图象经过直线y=x+1与y=3x+5的交点,那么y=kx的图象位于( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第一、二、三象限 |
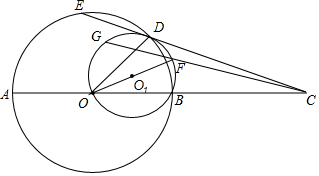 已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆.
已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆.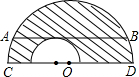 如图,两个半圆中,长为24的弦AB与直径CD平行且与小半圆相切,那么图中阴影部分的面积等于72π.
如图,两个半圆中,长为24的弦AB与直径CD平行且与小半圆相切,那么图中阴影部分的面积等于72π. 如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°.
如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°.