题目内容
13. 如图,∠AOB=90°,点P为∠AOB内一点.
如图,∠AOB=90°,点P为∠AOB内一点.(1)分别作出P点关于OA、OB的对称点P1,P2;(不写作法)
(2)求证:P1,O,P2三点在同一直线上;
(3)若OP=5,求P1P2的长度.
分析 (1)过P作BO的垂线,垂足为M,再截取PM=P1M,同方法作P点关于OA的对称点P1;
(2)根据轴对称的性质可得BO是P1P2的垂直平分线,AO是P1P的垂直平分线,再根据垂直平分线上的点到线段两端点距离相等可得P1O=PO,P2O=PO,然后可证明∠1+∠4=90°,再证明∠P1OP2=180°,从而可得P1,O,P2三点在同一直线上;
(3)首先证明四边形OMPN是矩形,可得∠MPN=90°,再根据直角三角形斜边上的中线等于斜边的一半可得OP=$\frac{1}{2}$P1P2,进而可得答案.
解答 (1)解:如图所示:
(2)证明:
∵P点关于OA、OB的对称点P1,P2,
∴BO是P2P的垂直平分线,AO是P1P的垂直平分线,
∴P1O=PO,P2O=PO,
∴∠1=∠2,∠3=∠4,
∵∠AOB=90°,
∴∠2+∠3=90°,
∴∠1+∠4=90°,
∴∠P1OP2=180°,
∴P1,O,P2三点在同一直线上;
(3)解:∵P点关于OA、OB的对称点P1,P2,
∴∠PMO=∠PNO=90°,
∵∠AOB=90°,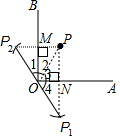
∴四边形OMPN是矩形,
∴∠MPN=90°,
∵P1O=PO,P2O=PO,
∴P1O=P2O=PO,
∴PO是P1P2的中线,
∴OP=$\frac{1}{2}$P1P2,
∵OP=5,
∴P1P2=10.
点评 此题主要考查了作图--轴对称变换,以及直角三角形的性质,关键是掌握对称轴是对称点连线的垂直平分线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.三棱柱的顶点个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.下列运算正确的是( )
| A. | (m2n)3=m5n3 | B. | -2x2+5x2=3x2 | C. | (-y2)3=y6 | D. | a2•a3=a6 |

 已知平面上点A,B,C,D.按下列要求画出图形:
已知平面上点A,B,C,D.按下列要求画出图形: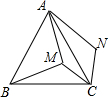 如图,M为等边△ABC内部的一点,且MA=8,MB=10,MC=6,将△BMC绕点C顺时针旋转得到△ANC.下列说法中:①MC=NC;②AM=AN;③S四边形AMCN=S△ABC-S△ABM;④∠AMC=120°.正确的有①③.(请填上番号)
如图,M为等边△ABC内部的一点,且MA=8,MB=10,MC=6,将△BMC绕点C顺时针旋转得到△ANC.下列说法中:①MC=NC;②AM=AN;③S四边形AMCN=S△ABC-S△ABM;④∠AMC=120°.正确的有①③.(请填上番号)
 已知一次函数y1=-x+1,y2=2x-5的图象如图所示,根据图象,解决下列问题:
已知一次函数y1=-x+1,y2=2x-5的图象如图所示,根据图象,解决下列问题: