题目内容
1. 已知平面上点A,B,C,D.按下列要求画出图形:
已知平面上点A,B,C,D.按下列要求画出图形:(1)作直线AB,射线CB;
(2)取线段AB的中点E,连接DE并延长与射线CB交于点O;
(3)量出∠AED和∠BEO的度数,并写出它们的数量关系;
(4)请画出从点A到射线CB的最短路线,并写出画图的依据.
分析 (1)作直线AB,直线没有端点,可以向两方无限延伸,射线CB,以A为端点,可以向一方无限延伸;
(2)取线段AB的中点E,画线段DE,再沿DE方向延长,与CB的交点记为O;
(3)利用量角器量出∠AED和∠BEO的度数,可得∠AED=∠BEO;
(4)根据垂线段最短,过A作AF垂直于BC.
解答 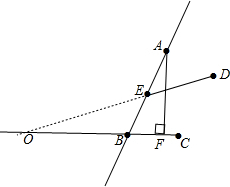 解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)∠AED=34°∠OEB=34°,∠AED=∠BEO;
(4)如图所示:AF就是从点A到射线CB的最短路线,根据是垂线段最短.
点评 此题主要考查了直线、射线和线段,以及垂线段的性质,关键是掌握三线的性质:直线没有端点,可以向两方无限延伸;射线有1个端点,可以向一方无限延伸;线段有2个端点,本身不能向两方无限延伸.

练习册系列答案
相关题目
11.下面计算结果正确的是( )
| A. | b3•b3=2b3 | B. | (a5)2=a7 | C. | (ab2)3=a3b6 | D. | (-2a)2=-4a2 |
12.已知反比例函数$y=\frac{5}{x}$的图象上有两点A(1,m),B(2,n),则m与n的大小关系是( )
| A. | m>n | B. | m<n | C. | m=n | D. | 不能确定 |
9.下列方程中,有一个根为-1的方程是( )
| A. | x2-x=0 | B. | x2-7x+6=0 | C. | 2x2-3x-5=0 | D. | 3x2+2x-5=0 |
16.2x2-x-6的一个因式是( )
| A. | x-2 | B. | 2x+1 | C. | x+3 | D. | 2x-3 |
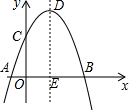 如图,在平面直角坐标系中,已知抛物线与x轴交于点A(-1,0)和点B,与y轴交于点C(0,2),对称轴为直线x=1,对称轴交x轴于点E.
如图,在平面直角坐标系中,已知抛物线与x轴交于点A(-1,0)和点B,与y轴交于点C(0,2),对称轴为直线x=1,对称轴交x轴于点E. 如图,∠AOB=90°,点P为∠AOB内一点.
如图,∠AOB=90°,点P为∠AOB内一点.