题目内容
11.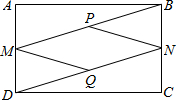 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.(1)求证:PM=PN;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.
分析 (1)连接MN,证明四边形AMNB是矩形,得出∠MNB=90°,根据直角三角形斜边上的中线性质即可得出结论;
(2)先证明四边形MPNQ是平行四边形,再由(1)即可得出结论.
解答 (1)证明:连接MN,如图所示: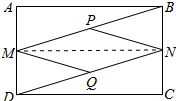 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC,AD=BC,
∵M、N分别是AD、BC的中点,
∴AM=DM=$\frac{1}{2}$AD,BN=CN=$\frac{1}{2}$BC,
∴AM=BN,
∴四边形AMNB是平行四边形,
∴平行四边形AMNB是矩形,
∴∠MNB=90°,
∵P是BM的中点,
∴PN=$\frac{1}{2}$BM=PM;
(2)四边形MPNQ是菱形;理由如下:
解:∵DM∥BN,DM=BN,
∴四边形BMDN是平行四边形,
∴BM∥ND,BM=ND,
又∵P、Q分别是BM、DN的中点,
∴PM=NQ,
∴四边形MPNQ是平行四边形,
由(1)得PM=PN,
∴四边形MPNQ时菱形.
点评 本题考查了矩形的性质、平行四边形的判定与性质、菱形的判定以及直角三角形斜边上的中线性质;证明四边形是平行四边形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
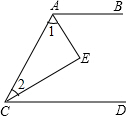 如图所示,根据题意填空已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.
如图所示,根据题意填空已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.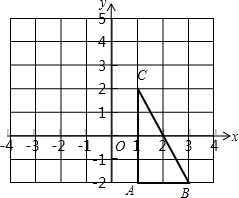 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,