题目内容
1.已知20a=100,5b=100,求a+b-ab的值.分析 先把20化为$(2{0}^{a})^{\frac{1}{a}}=10{0}^{\frac{1}{a}}$,5化为$({5}^{b})^{\frac{1}{b}}=10{0}^{\frac{1}{b}}$,利用同底数幂的乘法进行计算解答即可.
解答 解:∵$20=(2{0}^{a})^{\frac{1}{a}}=10{0}^{\frac{1}{a}}①$,
$5=({5}^{b})^{\frac{1}{b}}=10{0}^{\frac{1}{b}}$②,
∴①×②得:$20×5=10{0}^{\frac{1}{a}}×10{0}^{\frac{1}{b}}=10{0}^{\frac{1}{a}+\frac{1}{b}}=10{0}^{\frac{a+b}{ab}}$,
∴$\frac{a+b}{ab}=1$,
∴a+b=ab,
∴a+b-ab=0.
点评 此题考查同底数幂的乘法,关键是底数不变,指数相加的法则应用.

练习册系列答案
相关题目
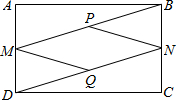 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
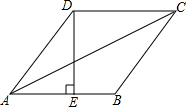 如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.
如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.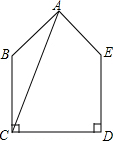 如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17.
如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17. 数学课上,李老师布置的作业是图中小黑板所示的内容,楚楚同学看错了第(2)题※中的数,求得(1)的一个解是x=2,翔翔同学由于看错了第(1)题中※中的数,求得(2)的一个解是x=3,你知道今天李老师布置作业的正确答案吗?请你解出来?
数学课上,李老师布置的作业是图中小黑板所示的内容,楚楚同学看错了第(2)题※中的数,求得(1)的一个解是x=2,翔翔同学由于看错了第(1)题中※中的数,求得(2)的一个解是x=3,你知道今天李老师布置作业的正确答案吗?请你解出来?