题目内容
2.若x,y,z满足$\left\{\begin{array}{l}{2x+3y-5z=0}\\{4x-y-3z=0}\end{array}\right.$,且xyz≠0,则$\frac{2x-3y}{4y+2z}$=-$\frac{1}{6}$.分析 通过解方程组,得到x、y以z表示的代数式,然后将其代入所求的分式,通过约分得到$\frac{2x-3y}{4y+2z}$的值.
解答 解:$\left\{\begin{array}{l}{2x+3y-5z=0(1)}\\{4x-y-3z=0(2)}\end{array}\right.$,
由(1)×2-(2),得
y=z.
由(1)+(2)×3,得
x=z,
所以$\frac{2x-3y}{4y+2z}$=$\frac{2z-3z}{4z+2z}$=-$\frac{1}{6}$.
故答案是:-$\frac{1}{6}$.
点评 本题考查了解三元一次方程组的解法,有加减法和代入法两种,一般选用加减法解方程组较简单.

练习册系列答案
相关题目
2.关于x,y的方程组$\left\{\begin{array}{l}{x+2y=m}\\{2x+y=1}\end{array}\right.$的解满足x-y=5,则m的值为( )
| A. | 4 | B. | 8 | C. | -4 | D. | -2 |
14.圆的周长公式为C=2πr,下列说法正确的是( )
| A. | 常量是2 | B. | 变量是C、π、r | C. | 变量是C、r | D. | 常量是2、r |
 如图,△ABC内接于⊙O,AB是直径,D是$\widehat{AC}$上的点,BD交AC于点E,过点B作⊙O的切线与AC的延长线交于点F,已知AB=5,sin∠CAB=$\frac{3}{5}$,求CF的长.
如图,△ABC内接于⊙O,AB是直径,D是$\widehat{AC}$上的点,BD交AC于点E,过点B作⊙O的切线与AC的延长线交于点F,已知AB=5,sin∠CAB=$\frac{3}{5}$,求CF的长.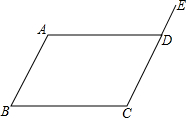 如图,AD∥BC,AB∥EC,∠B=60°,求∠ADE的度数.
如图,AD∥BC,AB∥EC,∠B=60°,求∠ADE的度数. 猜想并探究:
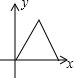
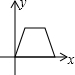
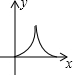
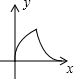
猜想并探究: 如图,△ABC与△DEF均为等腰三角形,且△ABC≌△DEF,∠B=∠DEF=90°,点B、C、E、F(C与E重合)在同一条直线上,△ABC从点C出发,沿射线BC方向匀速运动,△DEF的位置保持不动,当点B与点F重合时停止运动.设两个三角形重合部分的面积为y,△ABC平移的距离为x,下面能大致表示y与x间函数关系的图象是( )
如图,△ABC与△DEF均为等腰三角形,且△ABC≌△DEF,∠B=∠DEF=90°,点B、C、E、F(C与E重合)在同一条直线上,△ABC从点C出发,沿射线BC方向匀速运动,△DEF的位置保持不动,当点B与点F重合时停止运动.设两个三角形重合部分的面积为y,△ABC平移的距离为x,下面能大致表示y与x间函数关系的图象是( )