题目内容
19.解绝对值不等式:|x-2|+|x-4|≤3.分析 分别讨论①x≥4②2≤x<4③x<2,根据x的范围去掉绝对值,解出x,综合三种情况可得出x的最终范围.
解答 解:①当x≥4时,x-2+x-4≤3,
解得x≤$\frac{9}{2}$,
∴4≤x≤$\frac{9}{2}$;
②当2≤x<4时,x-2+4-x≤3,
解得x为范围内的所有实数;
∴2≤x<4;
③当x<2时,2-x+4-x≤3,
解得x≥$\frac{3}{2}$,
∴$\frac{3}{2}$≤x<2
∴不等式:|x-2|+|x-4|≤3的解集是$\frac{3}{2}$≤x≤$\frac{9}{2}$.
点评 本题考查了含绝对值符号的一元一次不等式,分类讨论是解题关键,意最后的解可以联合起来,难度很大.

练习册系列答案
相关题目
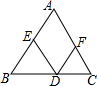 如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.
如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数. 如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.
如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.