题目内容
14. 如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.
如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.
分析 连接OA、OB、OE,如图,利用切线长定理得OA⊥PA,PB⊥PB,OE⊥CD,则根据“HL”可证明Rt△OAC≌△OEC,从而得到∠1=∠2,同理可得∠3=∠4,所以∠AOB=2∠COD=2y°,再根据四边形内角和得到∠P+∠AOB=180°,最后整理可得y与x之间的函数关系式.
解答 解;连接OA、OB、OE,如图,
∵PA,PB,CD是⊙O的三条切线,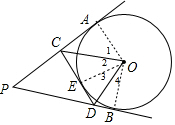
∴OA⊥PA,PB⊥PB,OE⊥CD,
在Rt△OAC和△OEC中
$\left\{\begin{array}{l}{OC=OC}\\{OA=OE}\end{array}\right.$,
∴Rt△OAC≌△OEC,
∴∠1=∠2,
同理可得∠3=∠4,
∴∠AOB=2∠COD=2y°,
∵∠P+∠AOB=180°,
∴x°+2y°=180°,
∴y=90-$\frac{1}{2}$x.
故答案为y=90-$\frac{1}{2}$x.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
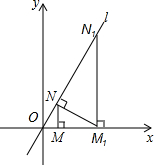 如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0).
如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0). 如图,△ABC∽△DBE,点E在AC上,∠ABC=∠DBE=90°,连接AD,求证:AD⊥AC.
如图,△ABC∽△DBE,点E在AC上,∠ABC=∠DBE=90°,连接AD,求证:AD⊥AC.