题目内容
1.解方程(若题目有要求,请按要求解答)(1)x2-4x+2=0(配方法);
(2)x2+3x+2=0.
分析 (1)把常数项2移项后,应该在左右两边同时加上一次项系数-4的一半的平方;
(2)将方程左边的多项式分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
解答 解:(1)把方程x2-4x2=0的常数项移到等号的右边,得
x2-4x=-2,
方程两边同时加上一次项系数一半的平方,得
x2-4x+4=2
配方,得
(x-2)2=2,
直接开平方,得
x-2=±$\sqrt{2}$,
解得,x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$;
(2)x2+3x+2=0,
因式分解得:(x+1)(x+2)=0,
解得:x1=-1,x2=-2.
点评 本题主要考查了解一元二次方程的知识,根据方程的特点选择合适的方法解一元二次方程是解决此类问题的关键.一般解一元二次方程的方法有直接开平方法、因式分解法、公式法、配方法.

练习册系列答案
相关题目
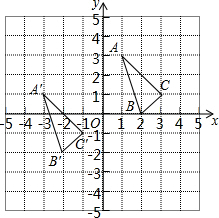 △ABC与△A'B'C'在平面直角坐标系中的位置如图.
△ABC与△A'B'C'在平面直角坐标系中的位置如图.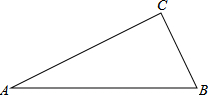 如图,在Rt△ABC中,∠C=90°,
如图,在Rt△ABC中,∠C=90°, 如图,用代数式表示图中阴影部分的面积,并求当a=4时阴影部分的面积(π取3).
如图,用代数式表示图中阴影部分的面积,并求当a=4时阴影部分的面积(π取3).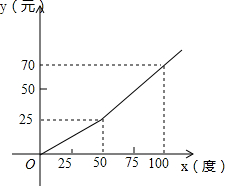 某地规定,每月每户的用电量xkW•h与应缴电费y元的关系如图所示,求出y与x之间的函数表达式.
某地规定,每月每户的用电量xkW•h与应缴电费y元的关系如图所示,求出y与x之间的函数表达式.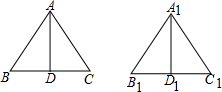 已知:如图,△ABC≌△A1B1C1,AD,A1D1分别是△ABC和△A1B1C1的高,求证:AD=A1D1.
已知:如图,△ABC≌△A1B1C1,AD,A1D1分别是△ABC和△A1B1C1的高,求证:AD=A1D1.