题目内容
已知一元二次方程ax2+bx+c=0的两根之比为m:n(a≠0,mn≠0),求证:mnb2=(m+n)2ac.
考点:根与系数的关系
专题:证明题
分析:设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,根据根与系数的关系得x1+x2=-
,x1x2=
,由于x1:x2=m:n,则x1=
x2,利用两根之和可表示求出x2=-
,x1=-
,然后利用两根之积得到-
•[-
]=
,再利用等式的性质即可得到结论.
| b |
| a |
| c |
| a |
| m |
| n |
| bn |
| a(m+n) |
| bm |
| a(m+n) |
| bm |
| a(m+n) |
| bn |
| a(m+n) |
| c |
| a |
解答:证明:设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,
根据题意,x1+x2=-
,x1x2=
,
∵x1:x2=m:n,
∴x1=
x2,
∴
x2+x2=-
,解得x2=-
,
∴x1=
•[-
]=-
,
∴-
•[-
]=
,
∴mnb2=(m+n)2ac.
根据题意,x1+x2=-
| b |
| a |
| c |
| a |
∵x1:x2=m:n,
∴x1=
| m |
| n |
∴
| m |
| n |
| b |
| a |
| bn |
| a(m+n) |
∴x1=
| m |
| n |
| bn |
| a(m+n) |
| bm |
| a(m+n) |
∴-
| bm |
| a(m+n) |
| bn |
| a(m+n) |
| c |
| a |
∴mnb2=(m+n)2ac.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.
如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.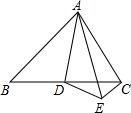 如图,在△ABC中,D是BC的中点,DE⊥AD,∠EAD=∠BAD.
如图,在△ABC中,D是BC的中点,DE⊥AD,∠EAD=∠BAD.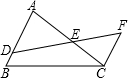 如图,在△ABC中,D是AB上的一点,DF交AC于点E,有下列3个论断:①DE=EF;
如图,在△ABC中,D是AB上的一点,DF交AC于点E,有下列3个论断:①DE=EF;