Question

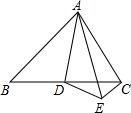如图，在△ABC中，D是BC的中点，DE⊥AD，∠EAD=∠BAD．
（1）求证：AB=AE+CE；
（2）已知AD=

1

2

BC，请判断△ACE形状并证明．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）延长ED交AB于点F，证得AF=AE，DF=DE和△BFD≌△CED，求得结论；
（2）求得∠ACE=90°，得出△ACE为直角三角形．

解答：（1）证明：如图，

延长ED交AB于点F，
∵∠EAD=∠BAD，DE⊥AD，
∴AF=AE，DF=DE，
又∵D是BC中点，
∴BD=CD，
在△BFD和△CED中，

DE=DF ∠BDF=∠CDE BD=CD

∴△BFD≌△CED（SAS），
∴EC=BF，
∴AB=AF+BF=AE+EC；

（2）∵AD=

1

2

BC，D为BC中点，
∴∠BAC=90°，∠ABC+∠ACB=90°，
又∵∠ABC=∠BCE，
∴∠ACE=90°，
∴△ACE为直角三角形．

点评：此题考查三角形全等的判定与性质，等腰三角形的判定与性质，以及直角三角形斜边上的中线的性质，注意作出辅助线，转化思路，解决问题．