Question

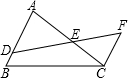如图，在△ABC中，D是AB上的一点，DF交AC于点E，有下列3个论断：①DE=EF；
②AE=CE；③AB∥CF．以其中一个论断为结论，其余两个论断为条件组成命
题．其中正确的有

 

个．

Answer 1

考点：全等三角形的判定与性质,命题与定理

专题：计算题

分析：根据全等三角形的判定与性质，可判断结论是否正确，根据真命题的定义，可得答案．

解答：解：以①②为条件，③为结论，是真命题，理由是：∵△AED≌△CEF（SAS），∠A=∠C，∴AB∥CF，故是真命题；
以①③为条件，②为结论，是真命题，理由是：∵AB∥CF，∴∠A=∠C，∴△AED≌△CEF（AAS），∴AE=CE，故是真命题；
乙②③为条件，①为结论，是真命题，理由是：∵AB∥CF，∴∠A=∠C，∴△AED≌△CEF（ASA），∴DE=FE，故是真命题；
故答案为：3．

点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．