题目内容
20. 如图,△ABC边长为6的等边三角形,△ACD是等腰三角形,且AD=CD=2$\sqrt{3}$,动点P,Q同时从点D出发,均以每秒1个单位的速度分别沿D→A→B和D→C→B的路线运动,设运动时间为t秒,△BPQ的面积为S,则S与t之间的函数关系图象大致为( )
如图,△ABC边长为6的等边三角形,△ACD是等腰三角形,且AD=CD=2$\sqrt{3}$,动点P,Q同时从点D出发,均以每秒1个单位的速度分别沿D→A→B和D→C→B的路线运动,设运动时间为t秒,△BPQ的面积为S,则S与t之间的函数关系图象大致为( )| A. |  | B. |  | C. |  | D. |  |
分析 根据题意可以分别求得点P从D到A和从点A到点B的解析式,从而可以求得对应的函数图象,从而可以得到哪个选项是正确的.
解答 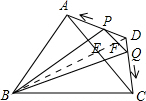 解:连接BD交AC于点E,交PQ于点F,如右图所示,
解:连接BD交AC于点E,交PQ于点F,如右图所示,
∵AB=BC=AC=6,AD=CD=2$\sqrt{3}$,BD⊥AC,BD⊥PQ,
∴AE=3,DE=$\sqrt{3}$,
∴tan∠DAE=$\frac{DE}{AE}=\frac{\sqrt{3}}{3}$,
∴∠DAE=30°,
当$0≤t≤2\sqrt{3}$时,
$S=\frac{PQ•BF}{2}=\frac{2t•cos30°•(6•sin60°+2\sqrt{3}•sin30°-t•sin30°)}{2}$=$\frac{2t•\frac{\sqrt{3}}{2}•(6×\frac{\sqrt{3}}{2}+2\sqrt{3}×\frac{1}{2}-t×\frac{1}{2})}{2}$=$-\frac{\sqrt{3}}{4}{t}^{2}+6t$=$-\frac{\sqrt{3}}{4}(t-4\sqrt{3})^{2}+12\sqrt{3}$;
当$2\sqrt{3}≤t≤6+2\sqrt{3}$时,
$S=\frac{BF•PQ}{2}=\frac{(6+2\sqrt{3}-t)•sin60°•(6+2\sqrt{3}-t)}{2}$=$\frac{\sqrt{3}}{4}(6+2\sqrt{3}-t)^{2}$,
故选C.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,求出各段对应的函数解析式,明确各段函数对应的函数图象.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
10.若二次函数y=-x2-3x+2的自变量x分别取x1、x2、x3,且x1、x2、x3,且0<x1<x2<x3,则对应的函数值y1、y2、y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y1<y3<y2 | D. | y2<y3<y1 |
15.如果一个三角形的两条边长分别为2和6,那么这个三角形第三边的长可能是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6.2 |
5.如果∠α=30°,那么∠α的余角是( )
| A. | 30° | B. | 150° | C. | 60° | D. | 70° |
 如图,在△ABC中,∠ACB=90°,将△ABC绕点C,按顺时针方向旋转得△A1B1C,且A1B1∥BC,∠ABB1=30°,求旋转角∠BCB1的大小.
如图,在△ABC中,∠ACB=90°,将△ABC绕点C,按顺时针方向旋转得△A1B1C,且A1B1∥BC,∠ABB1=30°,求旋转角∠BCB1的大小. 如图,直线l:y=-$\frac{3}{4}$x+b与x轴、y轴分别相交于点A、C,且△AOC的周长为24.
如图,直线l:y=-$\frac{3}{4}$x+b与x轴、y轴分别相交于点A、C,且△AOC的周长为24.