题目内容
14. 如图,直线l:y=-$\frac{3}{4}$x+b与x轴、y轴分别相交于点A、C,且△AOC的周长为24.
如图,直线l:y=-$\frac{3}{4}$x+b与x轴、y轴分别相交于点A、C,且△AOC的周长为24.(1)求直线l的函数关系式;
(2)过点(1,0)作x轴的垂线MN,求直线l关于直线MN对称的直线l′的函数关系式;
(3)若在直线1上存在一点P,使△POA的面积是△AOC的2倍,求点P的坐标.
分析 (1)根据题意求得OC=6,OA=8,即可求得b=6;
(2)求得C和A关于直线x=1的对称点为(2,6),(-6,0),然后根据待定系数法即可求得;
(3)根据题意求得P的纵坐标为±12,代入y=-$\frac{3}{4}$x+6即可求得横坐标.
解答 解:(1)∵直线l:y=-$\frac{3}{4}$x+b,
∴$\frac{OC}{OA}$=$\frac{3}{4}$,
设OC=3m,OA=4m,
∴AC=5m,
∵△AOC的周长为24,
∴3m+4m+5m=24,
解得m=2,
∴OC=6,OA=8,
∴C(0,6)A(8,0),
∴b=6,
∴直线l的函数关系式为y=-$\frac{3}{4}$x+6;
(2)∵C(0,6),A(8,0),
∴C和A关于直线x=1的对称点为(2,6),(-6,0),
设直线l′的函数关系式为y=mx+n,
把(2,6),(-6,0)代入得$\left\{\begin{array}{l}{6=2m+n}\\{0=-6m+n}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=\frac{3}{4}}\\{n=\frac{9}{2}}\end{array}\right.$
∴直线l′的函数关系式为y=$\frac{3}{4}$x+$\frac{9}{2}$;
(3)∵OA=8,OC=6,
∴△AOC的面积为:$\frac{1}{2}$×6×8=24,
∵△POA的面积是△AOC的2倍,
∴△POA的面积=48,
∴$\frac{1}{2}$OA•|yP|=48,
解得|yP|=12,
∴P(-8,12)或(24,-12).
点评 本题考查了待定系数法求一次函数的解析式以及一次函数的图象与几何变换,求得A,C的坐标是解题的关键.

 如图,△ABC边长为6的等边三角形,△ACD是等腰三角形,且AD=CD=2$\sqrt{3}$,动点P,Q同时从点D出发,均以每秒1个单位的速度分别沿D→A→B和D→C→B的路线运动,设运动时间为t秒,△BPQ的面积为S,则S与t之间的函数关系图象大致为( )
如图,△ABC边长为6的等边三角形,△ACD是等腰三角形,且AD=CD=2$\sqrt{3}$,动点P,Q同时从点D出发,均以每秒1个单位的速度分别沿D→A→B和D→C→B的路线运动,设运动时间为t秒,△BPQ的面积为S,则S与t之间的函数关系图象大致为( )




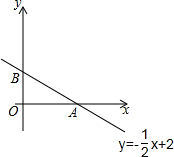 在平面直角坐标系中,已知直线l:y=-$\frac{1}{2}$x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
在平面直角坐标系中,已知直线l:y=-$\frac{1}{2}$x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.