题目内容

10．一个两位数，个位上的数字比十位上的数字小4，且个位数字与十位数字的平方和比这个两位数小4，若设个位数字为a，则可列方程为（　　）
A．a2（a-4）2=10（a-4）+a-4B．a2+（a+4）2=10a+a-4-4
C．a2+（a+4）2=10（a+4）+a-4D．a2+（a-4）2=10a+（a-4）-4

分析 根据个位数与十位数的关系，可知十位数为x+4，那么这两位数为：10（a+4）+a，这两个数的平方和为：a2+（a+4）2，再根据两数的值相差4即可得出答案．

解答 解：依题意得：十位数字为：a+4，这个数为：a+10（x+4）
这两个数的平方和为：a2+（a+4）2，
∵两数相差4，
∴a2+（a+4）2=10（a+4）+a-4．
故选C．

点评 本题考查了数的表示方法，要会利用未知数表示两位数，然后根据题意列出对应的方程求解．

练习册系列答案
相关题目
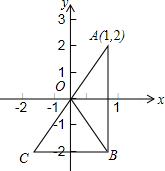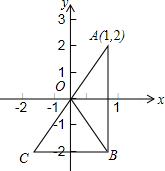20．如图，x轴是△AOB的对称轴，y轴是△BOC的对称轴，点A的坐标为（1，2），则点C的坐标为（　　）
A．（-1，-2）B．（1，-2）C．（-1，2）D．（-2，-1）
1．若△AED∽△ABC，AD=6cm，AC=12cm，则△AED与△ABC的相似比为1：2．
18．对于方程3x2-x-2=0，下列判断正确的是（　　）
A．一次项系数为1B．常数项是2C．二次项系数是3x2D．一次项是-x
5．关于x的一元二次方程x2+x+1=0的根的情况是（　　）
A．有两个不相等的正根B．有两个不相等的负根
C．没有实数根D．有两个相等的实数根
15．（1）比较下列两个数的大小：4＞$\sqrt{15}$；
（2）$\sqrt{15}$在哪两个连续整数之间？$\sqrt{15}$的整数部分是多少？
（3）若5-$\sqrt{15}$的整数部分是a，小数部分是b，试求a，b的值．
2．计算|2-$\sqrt{5}$|+|4-$\sqrt{5}$|的值是（　　）
A．-2B．2C．2$\sqrt{5}$-6D．6-2$\sqrt{5}$
19．先阅读下列一段文字，再回答后面的问题．
已知在平面内两点P1（x1，y1），P2（x2，y2），这两点间的距离P1P2=$\sqrt{（{x}_{2}-{x}_{1}）^{2}+（{y}_{2}-{y}_{1}）^{2}}$，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2-x1|或|y2-y1|．
（1）已知A（2，4），B（-3，-8），试求A，B两点间的距离；
（2）已知A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为-1，试求A，B两点间的距离．
20．如图，已知：在△ABC中，∠C=90°，∠A，∠B，∠C的对边为a，b，c，求证：a2+b2=c2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网