题目内容
19.先阅读下列一段文字,再回答后面的问题.已知在平面内两点P1(x1,y1),P2(x2,y2),这两点间的距离P1P2=$\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知A(2,4),B(-3,-8),试求A,B两点间的距离;
(2)已知A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A,B两点间的距离.
分析 (1)将点A、B的坐标代入两点间的距离公式进行解答即可;
(2)点A、B两点间的距|y2-y1|.
解答 解:(1)A,B两点间的距离=$\sqrt{(-3-2)^{2}+(-8-4)^{2}}$=13;
(3)A,B两点间的距离=|5-(-1)|=6.
点评 本题考查了两点间的距离公式.根据材料得到这两点间的距离P1P2=$\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$,或这两点间的距离P1P2=|x2-x1|或|y2-y1|是解题的关键.

练习册系列答案
相关题目
9. 如图,已知AB∥ED,∠ECF=65°,则∠BAF的度数为( )
如图,已知AB∥ED,∠ECF=65°,则∠BAF的度数为( )
 如图,已知AB∥ED,∠ECF=65°,则∠BAF的度数为( )
如图,已知AB∥ED,∠ECF=65°,则∠BAF的度数为( )| A. | 115° | B. | 65° | C. | 60° | D. | 25° |
10.一个两位数,个位上的数字比十位上的数字小4,且个位数字与十位数字的平方和比这个两位数小4,若设个位数字为a,则可列方程为( )
| A. | a2(a-4)2=10(a-4)+a-4 | B. | a2+(a+4)2=10a+a-4-4 | ||
| C. | a2+(a+4)2=10(a+4)+a-4 | D. | a2+(a-4)2=10a+(a-4)-4 |
14.电影院的第3排第6座表示为(3,6).若某同学的座位号为(4,2),那么该同学的位置是( )
| A. | 第2排第4座 | B. | 第4排第2座 | C. | 第4座第4排 | D. | 无法确定 |
4.在⊙O与⊙O′中,若∠AOB=∠A′O′B′,则AB与A′B′的关系为( )
| A. | AB=A′B′ | B. | AB>A′B′ | C. | AB<A′B′ | D. | 无法确定 |
11.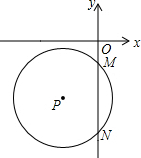 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=kx的图象经过点P,则k的值为( )
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=kx的图象经过点P,则k的值为( )
 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=kx的图象经过点P,则k的值为( )
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=kx的图象经过点P,则k的值为( )| A. | -$\frac{4}{7}$ | B. | -$\frac{7}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{7}{4}$ |
9.在Rt△ABC中,∠C=90°,tanA=$\frac{2}{3}$,AC=4,则BC等于( )
| A. | $\frac{8}{3}$ | B. | 2 | C. | 1 | D. | $\frac{7}{3}$ |
 如图,圆中有一条直径,三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条.
如图,圆中有一条直径,三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条.