题目内容
16.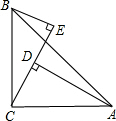 如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( )
如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( )| A. | 7 | B. | 8 | C. | 15 | D. | 22 |
分析 易证∠CAD=∠BCE,即可证明△CDA≌△BEC,可得CD=BE,CE=AD,根据DE=CE-CD,即可解题.
解答 解:∵∠ACB=90°,BE⊥CE于点E,AD⊥CE于点D,
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△CDA和△BEC中,
$\left\{\begin{array}{l}{∠CDA=∠BEC=90°}\\{∠CAD=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△CDA≌△BEC(AAS),
∴CD=BE,CE=AD,
∵DE=CE-CD,
∴DE=AD-BE,
∵AD=15cm,BE=7cm,
∴DE=15cm-7cm=8cm,
故选B
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(SSS、SAS、ASA、AAS和HL)和性质(全等三角形的对应边、对应角相等)是解题的关键.

练习册系列答案
相关题目
4.下列命题是假命题的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 正方形的对角线互相平分且垂直 | |
| C. | 菱形的对角线相等且互相垂直 | |
| D. | 对角线互相平分且相等的四边形是矩形 | |
| E. | 对角线互相平分且相等的四边形是矩形 |
8.若方程(x2+y2-1)2=16,则x2+y2=( )
| A. | 5或-3 | B. | 5 | C. | ±4 | D. | 4 |
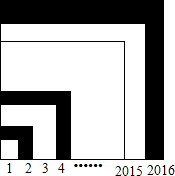 如图,边长分别为1,2,3,4,…,2015,2016的正方形叠放在一起,求图中阴影部分的面积.(提示:1+2+3…+n=$\frac{1}{2}$n(n+1))
如图,边长分别为1,2,3,4,…,2015,2016的正方形叠放在一起,求图中阴影部分的面积.(提示:1+2+3…+n=$\frac{1}{2}$n(n+1)) 如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=145°,则∠θ=70°.
如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=145°,则∠θ=70°.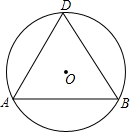 如图,已知⊙O的半径为2,弦AB的长为2$\sqrt{3}$,D是优弧$\widehat{ADB}$上的任意一点(点D不与A,B重合).
如图,已知⊙O的半径为2,弦AB的长为2$\sqrt{3}$,D是优弧$\widehat{ADB}$上的任意一点(点D不与A,B重合).