题目内容
8.若方程(x2+y2-1)2=16,则x2+y2=( )| A. | 5或-3 | B. | 5 | C. | ±4 | D. | 4 |
分析 方程两边开方,求出x2+y2的值,再判断即可.
解答 解:(x2+y2-1)2=16,
x2+y2-1=±4,
x2+y2=5,x2+y2=-3,
∵不论x、y为何值x2+y2都不等于-3,
即x2+y2=5,
故选B.
点评 本题考查了解一元二次方程的应用,熟记解一元一次方程的方法是解题的关键.

练习册系列答案
相关题目
19.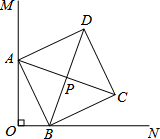 如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )
如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )
 如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )
如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )| A. | 点P始终在∠MON的平分线上,且线段OP的长有最小值等于$\sqrt{2}$ | |
| B. | 点P始终在∠MON的平分线上,且线段OP的长有最大值等于$\sqrt{2}$ | |
| C. | 点P不一定在∠MON的平分线上,但线段OP的长有最小值等于$\sqrt{2}$ | |
| D. | 点P运动路径无法确定 |
13.已知ab>0,a>0,ac>0,下列结论判断正确的是( )
| A. | b<0,c<0 | B. | b>0,c<0 | C. | b<0,c<0 | D. | b>0,c>0 |
20.二次函数y=2x2-6x+8的顶点坐标为( )
| A. | $({-\frac{3}{2},\frac{23}{4}})$ | B. | $({\frac{3}{2},\frac{23}{4}})$ | C. | $({\frac{3}{2},\frac{7}{2}})$ | D. | $({-\frac{3}{2},\frac{7}{2}})$ |
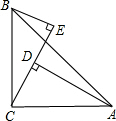 如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( )
如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( ) ,那么加上卡片上的数字;如果抽到的卡片形如
,那么加上卡片上的数字;如果抽到的卡片形如 ,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.