题目内容
7.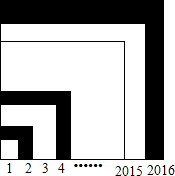 如图,边长分别为1,2,3,4,…,2015,2016的正方形叠放在一起,求图中阴影部分的面积.(提示:1+2+3…+n=$\frac{1}{2}$n(n+1))
如图,边长分别为1,2,3,4,…,2015,2016的正方形叠放在一起,求图中阴影部分的面积.(提示:1+2+3…+n=$\frac{1}{2}$n(n+1))
分析 一个阴影部分的面积等于第二个图形的面积减去第一个图形的面积,第二个阴影部分的面积等于第四个图形的面积减去第三个图形的面积,由此类推,最后一个阴影部分的面积等于最后一个图形的面积减去倒数第二个图形的面积,由此规律计算得出答案即可.
解答 解:图中阴影部分的面积为:
(22-1)+(42-32)+…+(20162-20152)
=(2+1)(2-1)+(4+3)(4-3)+…+(2016+2015)(2016-2015)
=1+2+3+4+…+2015+2016
=$\frac{1}{2}$×2016×(2016+1)
=2033136.
点评 此题考查图形的变化规律,得出每一个阴影部分的面积等于两个正方形面积的差,这样可以将阴影部分的面积看做边长为偶数的正方形的面积减去边长为奇数的正方形的面积解决问题.

练习册系列答案
相关题目
19.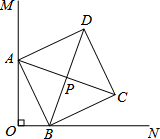 如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )
如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )
 如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )
如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )| A. | 点P始终在∠MON的平分线上,且线段OP的长有最小值等于$\sqrt{2}$ | |
| B. | 点P始终在∠MON的平分线上,且线段OP的长有最大值等于$\sqrt{2}$ | |
| C. | 点P不一定在∠MON的平分线上,但线段OP的长有最小值等于$\sqrt{2}$ | |
| D. | 点P运动路径无法确定 |

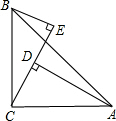 如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( )
如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( ) ,那么加上卡片上的数字;如果抽到的卡片形如
,那么加上卡片上的数字;如果抽到的卡片形如 ,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.