题目内容
3.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,不能判断△ABC为直角三角形的是( )| A. | ∠A:∠B:∠C=3:4:5 | B. | a2=1,b2=2,c2=3 | C. | (b+c)(b-c)=a2 | D. | ∠A-∠B=∠C |
分析 利用直角三角形的定义和勾股定理的逆定理逐项判断即可.
解答 解:A、∵∠A:∠B:∠C=3:4:5,且∠A+∠B+∠C=180°,可求得∠C≠90°,故△ABC不是直角三角形;
B、∵a2=1,b2=2,c2=3,∴a2+b2=3=c2,故△ABC是直角三角形;
C、由条件可得到a2+c2=b2,满足勾股定理的逆定理,故△ABC是直角三角形;
D、由条件∠A-∠B=∠C,且∠A+∠B+∠C=180°,可求得∠A=90°,故△ABC是直角三角形;
故选A.
点评 本题主要考查直角三角形的判定方法,掌握判定直角三角形的方法是解题的关键,可以利用定义也可以利用勾股定理的逆定理.

练习册系列答案
相关题目
13.下列多项式:(1)x3+xy-y2;(2)-x2+2xy-y2;(3)xy+x2+y2;(4)1-x+$\frac{{x}^{2}}{4}$中,能用完全平方公式分解因式的是( )
| A. | (1)(2) | B. | (1)(3) | C. | (1)(4) | D. | (2)(4) |
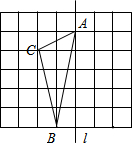 如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.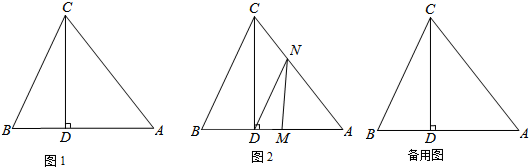
 用一个圆心角为120°、半径为18cm的扇形作一个圆锥的侧面.求圆锥底面积圆的半径R.
用一个圆心角为120°、半径为18cm的扇形作一个圆锥的侧面.求圆锥底面积圆的半径R.