题目内容
7．用同样大小的“△”按如图所示的方式摆图形，第1个图形需要2个“△”，第2个图形需要6个“△”，第3个图形需要12个“△”，按照这样的规律摆下去，则第n个图形需要“△”n+n2个（用含n的式子表示）．
分析 第一个图形有1+12=2个三角形，第二个图形有2+22=6个三角形，第三个图形有3+32=12个三角形，以此类推，得到结论．
解答 解：第一个图形有1+12=2个三角形，
第二个图形有2+22=6个三角形，
第三个图形有3+32=12个三角形，
…
第n个图形有n+n2个三角形，
故答案为：n+n2．
点评 此题考查了图形的变化类问题，解题的关键是仔细读题，找到三角形个数的通项公式，难度不大．
练习册系列答案
同步练习强化拓展系列答案
相关题目
17．已知菱形ABCD，∠A等于120°，AB=6，E为AB的中点，F、M分别在AD、DC上滑动，且FM=3，则△FME面积的最大值为（ ）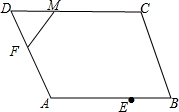 
| A． | 12 | B． | 6 | C． | $\frac{7}{4}$$\sqrt{3}$ | D． | $\frac{9}{2}$$\sqrt{3}$ |
18．检验下列各方程的解正确的是（ ）
| A． | 2x-1=$\frac{2}{3}-3x（x=\frac{1}{3}）$ | B． | 1=$\frac{x}{2}-4$（x=-10） | ||
| C． | 4x+2=-x-3（x=1） | D． | 0.48x-6=0.02x（x=1.2） |
15．已知$\frac{a}{2}$=$\frac{b}{3}$≠0，则$\frac{a+2b}{b}$的值为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{5}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
已知，如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点，求证：