题目内容
12. 如图,在平面直角坐标系中,反比例函数y=$\frac{m}{x}$与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(-3,2),BC⊥y轴于点C,且OC=6BC,直线AB交x轴于点D.
如图,在平面直角坐标系中,反比例函数y=$\frac{m}{x}$与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(-3,2),BC⊥y轴于点C,且OC=6BC,直线AB交x轴于点D.(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)写出不等式$\frac{m}{x}$>kx+b的解集.
分析 (1)待定系数法把A点坐标代入反比例函数解析式计算即可得出反比例函数的解析式;然后设B(a,-6a),把B(a,-6a)代入求得的解析式即可求得b的坐标,然后根据待定系数法即可求得一次函数的解析式;
(2)求得D的坐标,然后根据S△AOB=S△AOD+S△BOD求得即可;
(3)根据图象即可求得.
解答 解:(1)∵一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-3,2),
∴2=$\frac{m}{-3}$,解得m=-6,
∴反比例函数解析式为y=-$\frac{6}{m}$,
∵BC⊥y轴于点C,且OC=6BC,
∴设B(a,-6a),
把B(a,-6a)代入y=-$\frac{6}{x}$得,-6a=-$\frac{6}{a}$,
∴a2=1,
∴a=1
∴B(1,-6),
∵一次函数y=kx+b图象经过A(-3,2)、B(1,-6),
∴$\left\{\begin{array}{l}{-3k+b=2}\\{k+b=-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=-4}\end{array}\right.$,
∴一次函数y=-2x-4;
(2)由直线y=-2x-4可知D(-2,0),
∴S△AOB=S△AOD+S△BOD=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×6=8;
(3)不等式$\frac{m}{x}$>kx+b的解集是:-3<x<0或x>1.
点评 本题考查了反比例函数和一次函数的交点,待定系数法求一次函数和反比例函数的解析式以及函数和不等式的关系,熟练掌握待定系数法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.汤姆在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表:
(1)汤姆以折扣价购买商品A、B是第几次购物?为什么;
(2)求商品A、B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品的?
| 商品A的数量(个) | 商品B的数量(个) | 总费用(元) | |
| 第一次购物 | 5 | 3 | 810 |
| 第二次购物 | 4 | 5 | 960 |
| 第三次购物 | 8 | 9 | 1080 |
(2)求商品A、B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品的?
 如图,在等腰△ABC中,AB=AC,分别作CD⊥AB,BE⊥AC,EG⊥AB,DF⊥AC.求证:四边形MDNE是菱形.
如图,在等腰△ABC中,AB=AC,分别作CD⊥AB,BE⊥AC,EG⊥AB,DF⊥AC.求证:四边形MDNE是菱形.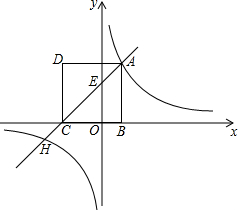 如图,已知四边形ABCD是正方形,边BC在x轴上,点A在反比例函数y=$\frac{4}{x}$的图象上,直线AC与y轴交于点E(0,3),与反比例函数y=$\frac{4}{x}$的图象的另一个交点为H.
如图,已知四边形ABCD是正方形,边BC在x轴上,点A在反比例函数y=$\frac{4}{x}$的图象上,直线AC与y轴交于点E(0,3),与反比例函数y=$\frac{4}{x}$的图象的另一个交点为H. 如图,已知AB∥CD,∠BEF=∠BFE,∠DEG=∠DGK,证明:EG⊥EF.
如图,已知AB∥CD,∠BEF=∠BFE,∠DEG=∠DGK,证明:EG⊥EF.