题目内容
某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
若该店购进螺母数量是螺丝数量的3倍还多200个,且两种配件的总量不超过3000个,该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:
(1)若设购进螺丝x个,总获利为y元,求y与x的函数关系式,并求出自变量x的取值范围;
(2)怎样进货,才能获得最大利润?最大利润是多少?
| 原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
| 螺丝 | 0.5 | 1.0 | 2.0 |
| 螺母 | 0.2 | 0.6 | 2.0 |
(1)若设购进螺丝x个,总获利为y元,求y与x的函数关系式,并求出自变量x的取值范围;
(2)怎样进货,才能获得最大利润?最大利润是多少?
考点:一次函数的应用
专题:
分析:(1)根据总获利等于配套销售的销售额和零售的销售额减去螺丝与螺母进价列式整理即可,再根据两种配件的总量列出不等式,求解即可得到x的取值范围;
(2)根据一次函数的增减性求解即可.
(2)根据一次函数的增减性求解即可.
解答:解:(1)y=
x×2+
x×1+
×(3x-200-2x)×0.6-
x×0.5-
×(3x-200)×0.2,
=x+0.5x+0.3x-60-0.25x-0.3x+20,
=1.25x-40,
∵两种配件的总量不超过3000个,
∴x+(3x-200)≤3000,
解得x≤800,
∴x的取值范围是0<x≤800;
(2)∵k=1.25>0,
∴y随x的增大而增大,
∴当x=800时,获得利润最大,最大利润为1.25×800-40=960元.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=x+0.5x+0.3x-60-0.25x-0.3x+20,
=1.25x-40,
∵两种配件的总量不超过3000个,
∴x+(3x-200)≤3000,
解得x≤800,
∴x的取值范围是0<x≤800;
(2)∵k=1.25>0,
∴y随x的增大而增大,
∴当x=800时,获得利润最大,最大利润为1.25×800-40=960元.
点评:本题考查了一次函数的应用,主要是利用一次函数的增减性求最值问题,难点在于表示出配套和零售的螺丝和螺母的销售额.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
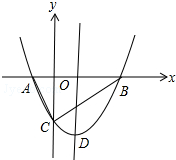 如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).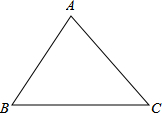 从三角形木板上截下一块圆形的木板,
从三角形木板上截下一块圆形的木板,