题目内容
文明餐桌，拒绝“剩”宴！某中学发起“拒绝浪费，从我做起”的“光盘”行动！学校为了了解学生生活习惯是否符合“光盘”观念，在全校进行了一次问卷调查，若学生生活习惯符合“关盘”观念，则称其为“光盘族”；否则，称其为“非光盘族”．学校有七、八、九三个年级，经过统计，将全校的“光盘族”人数按年级绘制成如两幅统计图：（1）根据图①、图②，计算七年级的“光盘族”人数；
（2）补全以上两个统计图；
（3）学校为了提倡和宣传“光盘”行动，从各年级的“光盘族”中各选出2人在学校进行“光盘”行动宣传工作，并从中再选2人到社区进行宣传．请利用树状图或列表法求出：选为社区宣传的同学来自同一年级的概率是多少？
考点：条形统计图,扇形统计图,列表法与树状图法
专题：
分析：（1）根据条形统计图得到八年级“光盘族”的人数为240人，根据扇形统计图得到所占的百分比为30%，求出“光盘族”的总人数，得到七年级“光盘族”的人数；
（2）根据求出七年级的人数，以及总人数，补全两个统计图即可；
（3）根据题意列出表格，得出所有可能的结果，找出在同一年级的情况个数，即可求出所求的概率．
（2）根据求出七年级的人数，以及总人数，补全两个统计图即可；
（3）根据题意列出表格，得出所有可能的结果，找出在同一年级的情况个数，即可求出所求的概率．
解答：解：（1）240÷30%=800（人），
则七年级“光盘族”的人数为800-（240+360）=200人；
（2）九年级所占的百分比为
×100%=45%；
七年级所占的百分比为
×100%=25%，
补全如下：
（3）列表得：
所有的可能为30种，其中所选同学都来自同一年级的有6种，
则P（所选两位同学都来自同一年级）=
=
．
则七年级“光盘族”的人数为800-（240+360）=200人；
（2）九年级所占的百分比为
| 360 |
| 800 |
七年级所占的百分比为
| 200 |
| 800 |
补全如下：
（3）列表得：
| 七1 | 七2 | 八1 | 八2 | 九1 | 九2 | |
| 七1 | --- | （七2，七1） | （八1，七1） | （八2，七1） | （九1，七1） | （九2，七1） |
| 七2 | （七1，七2） | --- | （八1，七2） | （八2，七2） | （九1，七2） | （九2，七2） |
| 八1 | （七1，八1） | （七2，八1） | --- | （八2，八1） | （九1，八1） | （九2，八1） |
| 八2 | （七1，八2） | （七2，八2） | （八1，八2） | --- | （九1，八2） | （九2，八2） |
| 九1 | （七1，九1） | （七2，九1） | （八1，九1） | （八2，九1） | --- | （九2，九1） |
| 九2 | （七1，九2） | （七2，九2） | （八1，九2） | （八2，九2） | （九1，九2） | --- |
则P（所选两位同学都来自同一年级）=
| 6 |
| 30 |
| 1 |
| 5 |
点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．除此之外，本题也考查了列表法与树状图法，概率公式，概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
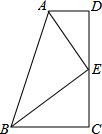如图，已知四边形ABCD中，∠D=∠C=90°，AE平分∠BAD，点E是DC的中点，且E在DC上．
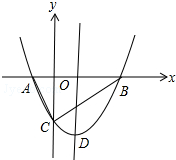如图，抛物线y=x2+bx-2与x轴交于A，B两点，与y轴交于C点，且A（-1，0）．