题目内容
2.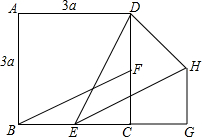 如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.
如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.
分析 设BE=x,△DHE的面积为y,通过三角形DHE的面积=三角形CDE的面积+梯形CDHG的面积-三角形EGH的面积,得出关于x,y的函数关系式,然后根据函数的性质求出y取最小值时x的值,并求出此时y的值.
解答 解:设BE=x,△DHE的面积为y,
依题意y=S△CDE+S梯形CDHG-S△EGH,
=$\frac{1}{2}$×3a×(3a-x)+$\frac{1}{2}$×(3a+x)×x-$\frac{1}{2}$×3a×x,
=$\frac{1}{2}$x2-$\frac{3}{2}$ax+$\frac{9}{2}$a2,
y=$\frac{1}{2}$x2-$\frac{3}{2}$ax+$\frac{9}{2}$a2=$\frac{1}{2}$(x-1.5a)2+$\frac{27}{8}$a2,
当x=1.5a,即BE=$\frac{1}{2}$BC,E是BC的中点时,y取最小值,△DHE的面积y的最小值为$\frac{27}{8}$a2.
故答案为:$\frac{27}{8}$a2.
点评 本题主要考查了正方形的性质,二次函数的综合应用等知识点,正确得到x和y的二次函数关系式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.如果x=2是关于x的方程3-2x=x+a的解,那么a的值应是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
12.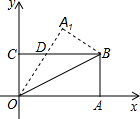 如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A($\sqrt{3}$,0)落在点A1处,已知点B的坐标是($\sqrt{3}$,1),则点A1的坐标是( )
如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A($\sqrt{3}$,0)落在点A1处,已知点B的坐标是($\sqrt{3}$,1),则点A1的坐标是( )
 如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A($\sqrt{3}$,0)落在点A1处,已知点B的坐标是($\sqrt{3}$,1),则点A1的坐标是( )
如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A($\sqrt{3}$,0)落在点A1处,已知点B的坐标是($\sqrt{3}$,1),则点A1的坐标是( )| A. | ($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$) | B. | ($\frac{{\sqrt{3}}}{2}$,$\frac{3}{2}$) | C. | ($\frac{{\sqrt{3}}}{2}$,2) | D. | ($\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}$) |
 作图题(不写作法,保留作图痕迹).
作图题(不写作法,保留作图痕迹).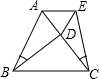 已知,如图△ABC为等边三角形,且∠ACE=∠ABD,CE=BD,试说明:
已知,如图△ABC为等边三角形,且∠ACE=∠ABD,CE=BD,试说明: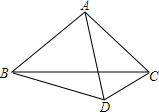 如图,△ABC是等边三角形,点D是△ABC外一点,试证明:DB+DC≥AD.
如图,△ABC是等边三角形,点D是△ABC外一点,试证明:DB+DC≥AD.